
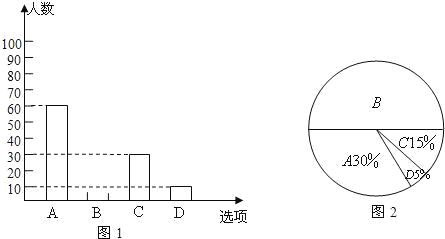
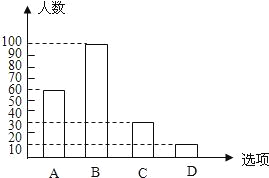
【題目】為了了解學生參加體育活動的情況,學校對學生進行隨機抽樣調查,其中一個問題是“你平均每天參加體育活動的時間是多少”,共有4個選項:A、1.5小時以上;B、1~1.5小時;C、0.5~1小時;D、0.5小時以下.圖1、2是根據調查結果繪制的兩幅不完整的統計圖,請你根據統計圖提供的信息,解答以下問題:
(1)本次一共調查了多少名學生?
(2)在圖1中將選項B的部分補充完整;
(3)若該校有3000名學生,你估計全校可能有多少名學生平均每天參加體育活動的時間在0.5小時以下?
【答案】(1)200;(2)圖形見解析;(3)學校有150人平均每天參加體育鍛煉在0.5小時以下.
【解析】
(1)讀圖可得:A類有60人,占30%即可求得總人數;
(2)計算可得:“B”是100人,據此補全條形圖;
(3)用樣本估計總體,若該校有3000名學生,則學校有3000×5%=150人平均每天參加體育鍛煉在0.5小時以下.
解:(1)讀圖可得:A類有60人,占30%;則本次一共調查了60÷30%=200人;本次一共調查了200位學生;
(2)“B”有200-60-30-10=100人,畫圖正確;
(3)用樣本估計總體,每天參加體育鍛煉在0.5小時以下占5%;則3000×5%=150,
學校有150人平均每天參加體育鍛煉在0.5小時以下.


科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系xOy中,A、B為x軸上兩點,C、D為y軸上的兩點,經過點A、C、B的拋物線的一部分c1與經過點A、D、B的拋物線的一部分c2組合成一條封閉曲線,我們把這條封閉曲線成為“蛋線”.已知點C的坐標為(0,﹣![]() ),點M是拋物線C2:y=mx2﹣2mx﹣3m(m<0)的頂點.
),點M是拋物線C2:y=mx2﹣2mx﹣3m(m<0)的頂點.
(1)求A、B兩點的坐標;
(2)“蛋線”在第四象限上是否存在一點P,使得△PBC的面積最大?若存在,求出△PBC面積的最大值;若不存在,請說明理由;
(3)當△BDM為直角三角形時,求m的值.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某游泳館普通票價20元![]() 張,暑假為了促銷,新推出兩種優惠卡:
張,暑假為了促銷,新推出兩種優惠卡:
![]() 金卡售價600元
金卡售價600元![]() 張,每次憑卡不再收費.
張,每次憑卡不再收費.
![]() 銀卡售價150元
銀卡售價150元![]() 張,每次憑卡另收10元.
張,每次憑卡另收10元.
暑假普通票正常出售,兩種優惠卡僅限暑假使用,不限次數![]() 設游泳x次時,所需總費用為y元
設游泳x次時,所需總費用為y元
![]() 分別寫出選擇銀卡、普通票消費時,y與x之間的函數關系式;
分別寫出選擇銀卡、普通票消費時,y與x之間的函數關系式;
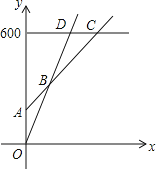
![]() 在同一坐標系中,若三種消費方式對應的函數圖象如圖所示,請求出點A、B、C的坐標;
在同一坐標系中,若三種消費方式對應的函數圖象如圖所示,請求出點A、B、C的坐標;
![]() 請根據函數圖象,直接寫出選擇哪種消費方式更合算.
請根據函數圖象,直接寫出選擇哪種消費方式更合算.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】溫度通常有兩種表示方法:華氏度(單位:℉)與攝氏度(單位:℃),已知華氏度數![]() 與攝氏度數
與攝氏度數![]() 之間是一次函數關系,下表列出了部分華氏度與攝氏度之間的對應關系:
之間是一次函數關系,下表列出了部分華氏度與攝氏度之間的對應關系:
攝氏度數 | … | 0 | … | 35 | … | 100 | … |
華氏度數 | … | 32 | … | 95 | … | 212 | … |
(1)選用表格中給出的數據,求y關于x的函數解析式;
(2)有一種溫度計上有兩個刻度,即測量某一溫度時左邊是攝氏度,右邊是華氏度,那么在多少攝氏度時,溫度計上右邊華氏度的刻度正好比左邊攝氏度的刻度大56?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(10分)下面的圖形是由邊長為l的正方形按照某種規律排列而組成的.
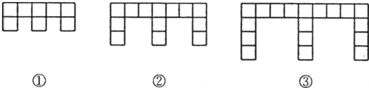
(1)觀察圖形,填寫下表:
圖形 | ① | ② | ③ |
正方形的個數 | 8 |
|
|
圖形的周長 | 18 |
|
|
(2)推測第n個圖形中,正方形的個數為 ,周長為 (都用含n的代數式表示).
(3)這些圖形中,任意一個圖形的周長y與它所含正方形個數x之間的關系可表示為y= .
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為推動陽光體育活動的廣泛開展,引導學生積極參加體育鍛煉,學校準備購買一批運動鞋供學生借用.現從各年級隨機抽取了部分學生的鞋號,繪制了如下的統計圖①和圖②,請根據圖中提供的信息,解答下列問題:

(1)本次接受隨機抽樣調查的學生人數為 人,圖①中的m的值為 ,圖①中“38號”所在的扇形的圓心角度數為 ;
(2)本次調查獲取的樣本數據的眾數是 ,中位數是 ;
(3)根據樣本數據,若學校計劃購買200雙運動鞋,建議購買36號運動鞋多少雙?
查看答案和解析>>
科目:初中數學 來源: 題型:
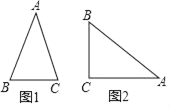
【題目】背景閱讀:我們在教材24.3已經知道了直角三角形中銳角的三角函數的概念,類似地,我們在等腰三角形中建立邊角之間的關系,即等腰三角形中底邊與腰的比叫做頂角的正對,記作:sad.如圖1,在△ABC中,AB=AC,頂角A的正對記作:sadA,這時sadA=![]() =
=![]() .
.
問題解決:
(1)若頂角A=60°,求sadA的值;
(2)若90°<∠A<180°,求∠A的正對sadA的取值范圍;
合作交流:
(3)如圖2,在Rt△ABC中,∠ACB=90°,若sinA=![]() ,試求以AC為腰的等腰三角形中,頂角A的正對sadA的值.
,試求以AC為腰的等腰三角形中,頂角A的正對sadA的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】瑞士著名數學家歐拉發現:簡單多面體的頂點數V、面數F及棱數E之間滿足一種有趣的關系:V+F﹣E=2,這個關系式被稱為歐拉公式.比如:正二十面體(如右圖),是由20個等邊三角形所組成的正多面體,已知每個頂點處有5條棱,則可以通過歐拉公式算出正二十面體的頂點為_____個.那么一個多面體的每個面都是五邊形,每個頂點引出的棱都有3條,它是一個_____面體.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com