
【題目】仙降是瑞安重要的制鞋基地,其生產的鞋子暢銷世界各地,某制鞋企業欲將![]() 件產品運往
件產品運往![]() 三地銷售,運往
三地銷售,運往![]() 地的費用為18元/件,運往
地的費用為18元/件,運往![]() 地的費用為20元/件,運往
地的費用為20元/件,運往![]() 地的費用為17元/件,要求運往
地的費用為17元/件,要求運往![]() 地的件數與運往
地的件數與運往![]() 地的件數相同. 設安排
地的件數相同. 設安排![]() 件產品運往
件產品運往![]() 地.
地.
(1)若![]() ①運往
①運往![]() 地件數為 件(用含
地件數為 件(用含![]() 的代數式表示);②若總運費不超過1850元,則運往
的代數式表示);②若總運費不超過1850元,則運往![]() 地至少有多少件?
地至少有多少件?
(2)若總運費為1900元,則![]() 的最大值為 .(直接寫出答案)
的最大值為 .(直接寫出答案)
科目:初中數學 來源: 題型:
【題目】某市為了鼓勵居民節約用水,決定實行兩級收費制度,若每月用水量不超過14噸(含14噸),則每噸按政府補貼優惠價m元收費;若每月用水量超過14噸,則超過部分每噸按市場價n元收費.小明家3月份用水20噸,交水費49元;4月份用水18噸,交水費42元.
(1)求每噸水的政府補貼優惠價m和市場價n分別是多少元?
(2)小明家5月份交水費70元,則5月份他家用了多少噸水?
查看答案和解析>>
科目:初中數學 來源: 題型:
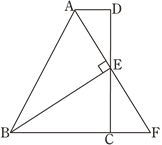
【題目】如圖,在四邊形ABCD中,AD∥BC,E為CD的中點,連接AE、BE,BE⊥AE,延長AE交BC的延長線于點F. 已知AD=2cm,BC=5cm.
(1)求證:FC=AD;
(2)求AB的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知一拋物線形大門,其地面寬度![]() .一同學站在門內,在離門腳
.一同學站在門內,在離門腳![]() 點
點![]() 遠的
遠的![]() 處,垂直地面立
處,垂直地面立
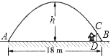
起一根![]() 長的木桿,其頂端恰好頂在拋物線形門上
長的木桿,其頂端恰好頂在拋物線形門上![]() 處.根據這些條件,請你求出該大門的高
處.根據這些條件,請你求出該大門的高![]() .
.
查看答案和解析>>
科目:初中數學 來源: 題型:
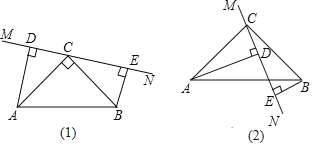
【題目】在△ABC中,∠ACB=90![]() ,AC=BC,直線MN經過點C,且AD⊥MN于D,BE⊥MN于E.
,AC=BC,直線MN經過點C,且AD⊥MN于D,BE⊥MN于E.
(1)當直線MN如圖(1)的位置時,
求證:①△ADC≌△CEB ②DE=AD+BE
(2)當直線MN繞點C旋轉到圖(2)的位置時,直接寫出DE、AD、BE三者之間的關系 .
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知反比例函數![]() 的圖像與一正比例函數的圖像相交于點
的圖像與一正比例函數的圖像相交于點![]() ,點
,點![]() 的坐標是
的坐標是![]() .
.
(1)求正比例函數的解析式;
(2)若正比例函數![]() 的圖像與反比例函數
的圖像與反比例函數![]() 的圖像在第一象限內交于點
的圖像在第一象限內交于點![]() ,過點
,過點![]() 作
作![]() 軸的垂線,
軸的垂線,![]() 為垂足,且交直線
為垂足,且交直線![]() 于點
于點![]() ,過點
,過點![]() 作
作![]() 軸的垂線,
軸的垂線,![]() 為垂足,求梯形
為垂足,求梯形![]() 的面積;
的面積;
(3)連結![]() ,求
,求![]() 的面積.
的面積.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知等腰△ABC中,AB=AC,∠ABC的平分線交AC于D,過點A作AE // BC交BD的延長線于點E,∠CAE的平分線交BE于點F.
(1)①如圖,若∠BAC=36o,求證:BD=EF;
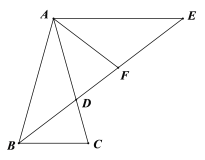
②如圖,若∠BAC=60o,求![]() 的值;
的值;
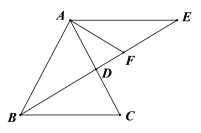
(2)如圖,若∠BAC=60o,過點D作DG// BC,交AB于點G,點N為BC中點,點P, M分別是GD, BG上的動點,且∠PNM=60°. 求證:AP=PN=MN.
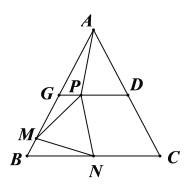
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,△ABC中,BA=BC,CO⊥AB于點O,AO=4,BO=6.
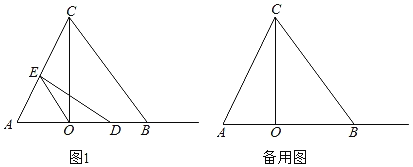
(1)求BC,AC的長;
(2)若點D是射線OB上的一個動點,作DE⊥AC于點E,連結OE.
①當點D在線段OB上時,若△AOE是以AO為腰的等腰三角形,請求出所有符合條件的OD的長.
②設DE交直線BC于點F,連結OF,CD,若S△OBF:S△OCF=1:4,則CD的長為 (直接寫出結果).
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com