【題目】在
中 ，
平分
交
于
，
的兩邊分別與
, 
相交于
，
兩點，且
.
（1）如圖，若
， 
，
，
，
.
①寫出
°，的長是 .
②求四邊形
的周長.
（2）如圖，過作
于
，作
于
，先補全圖乙再證明
.
【答案】（1）①90°，18，②30；（2）作圖見解析，證明見解析
【解析】
（1）①由直角三角形兩銳角互余可得
，結合直角三角形30度角的性質可得AB長，由平行的性質及角平分線的性質可得
，易得
的度數；②在①的基礎上，結合等角對等邊的性質可得
，
設
，根據直角三角形30度角的性質可得
，則
，
可得AM、MD、DN、AN的長，易得四邊形
的周長；
（3）利用HL定理可證
≌
，
，結合全等三角形對應邊相等的性質易證
.
解：①解：∵
, 
∴
∵
∴
，
又
∴
∴
又∵
平分
∴
∴
,
所以
90°，
的長是18.
②解：∵,
∴
∵
∴，
又
∴
∴
又∵平分
∴
∴
∴
在
中，設，則
∴
中, 
∴
∴
∴
∴
，
所以四邊形的周長=
（2）補全圖如圖所示
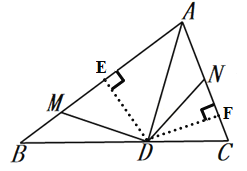
證明：由作圖知，
，
由已知，平分，
∴ ≌
又
.
每日10分鐘口算心算速算天天練系列答案科目：初中數學 來源： 題型：
【題目】如圖，△ABC中，∠ACB=90°，AC =3，BC =4，AB=5，BD平分∠ABC，如果M、N分別為BD、BC上的動點，那么CM+MN的最小值是____．
查看答案和解析>>
科目：初中數學 來源： 題型：
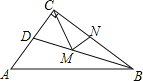
【題目】已知，在
中，
，
，
，垂足為點
，且
，連接
.
（1）如圖①，求證：
是等邊三角形；
（2）如圖①，若點
、
分別為
，
上的點，且
，求證：
；
（3）利用（1）（2）中的結論，思考并解答：如圖②，
為上一點，連結
，當
時，線段
，
，
之間有何數量關系，給出證明.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在矩形ABCD中，AB=2，點E在邊AD上，∠ABE=45°，BE=DE，連接BD，點P在線段DE上，過點P作PQ∥BD交BE于點Q，連接QD．設PD=x，△PQD的面積為y，則能表示y與x函數關系的圖象大致是（ ）
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】學生小明將線段
的垂直平分線
上的點
，稱作線段的“軸點”.其中，當
時，稱為線段的“長軸點”；當
時，稱為線段的“短軸點”.
（1）如圖1，點
，
的坐標分別為
，
，則在
，
，
，
中線段的“短軸點”是______.
（2）如圖2，點的坐標為
，點在
軸正半軸上，且
.
①若為線段的“長軸點”，則點的橫坐標
的取值范圍是（ ）
A.
B.
C.
D.或
②點
為軸上的動點，點，在線段的垂直平分線的同側.若
為線段的“軸點”，當線段
與
的和最小時，求點的坐標.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】已知拋物線C：y=x2﹣2x+1的頂點為P，與y軸的交點為Q，點F（1，
）．
（1）求tan∠OPQ的值；
（2）將拋物線C向上平移得到拋物線C′，點Q平移后的對應點為Q′，且FQ′=OQ′．
①求拋物線C′的解析式；
②若點P關于直線Q′F的對稱點為K，射線FK與拋物線C′相交于點A，求點A的坐標．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，△ABC和△ADE分別是以BC，DE為底邊且頂角相等的等腰三角形，點D在線段BC上，AF平分DE交BC于點F，連接BE，EF．
（1）CD與BE相等？若相等，請證明；若不相等，請說明理由；
（2）若∠BAC=90°，求證：BF2+CD2=FD2．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
