
【題目】程老師制作了如圖1所示的學具,用來探究“邊邊角條件是否可確定三角形的形狀”問題,操作學具時,點Q在軌道槽AM上運動,點P既能在以A為圓心、以8為半徑的半圓軌道槽上運動,也能在軌道槽QN上運動,圖2是操作學具時,所對應某個位置的圖形的示意圖.

有以下結論:
①當∠PAQ=30°,PQ=6時,可得到形狀唯一確定的△PAQ
②當∠PAQ=30°,PQ=9時,可得到形狀唯一確定的△PAQ
③當∠PAQ=90°,PQ=10時,可得到形狀唯一確定的△PAQ
④當∠PAQ=150°,PQ=12時,可得到形狀唯一確定的△PAQ
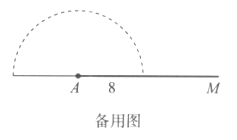
其中所有正確結論的序號是( )
A.②③B.③④C.②③④D.①②③④
【答案】C
【解析】
分別在以上四種情況下以P為圓心,PQ的長度為半徑畫弧,觀察弧與直線AM的交點即為Q點,作出![]() 后可得答案.
后可得答案.
如下圖,當∠PAQ=30°,PQ=6時,以P為圓心,PQ的長度為半徑畫弧,弧與直線AM有兩個交點,作出![]() ,發現兩個位置的Q都符合題意,所以
,發現兩個位置的Q都符合題意,所以![]() 不唯一,所以①錯誤.
不唯一,所以①錯誤.
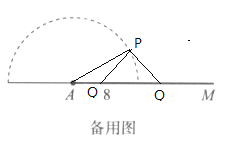
如下圖,當∠PAQ=30°,PQ=9時,以P為圓心,PQ的長度為半徑畫弧,弧與直線AM有兩個交點,作出![]() ,發現左邊位置的Q不符合題意,所以
,發現左邊位置的Q不符合題意,所以![]() 唯一,所以②正確.
唯一,所以②正確.
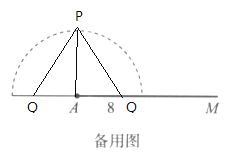
如下圖,當∠PAQ=90°,PQ=10時,以P為圓心,PQ的長度為半徑畫弧,弧與直線AM有兩個交點,作出![]() ,發現兩個位置的Q都符合題意,但是此時兩個三角形全等,所以形狀相同,所以
,發現兩個位置的Q都符合題意,但是此時兩個三角形全等,所以形狀相同,所以![]() 唯一,所以③正確.
唯一,所以③正確.
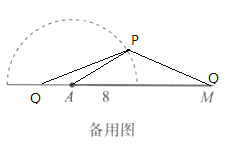
如下圖,當∠PAQ=150°,PQ=12時,以P為圓心,PQ的長度為半徑畫弧,弧與直線AM有兩個交點,作出![]() ,發現左邊位置的Q不符合題意,所以
,發現左邊位置的Q不符合題意,所以![]() 唯一,所以④正確.
唯一,所以④正確.
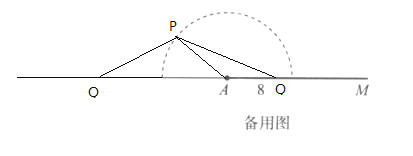
綜上:②③④正確.
故選C.


 發散思維新課堂系列答案
發散思維新課堂系列答案科目:初中數學 來源: 題型:
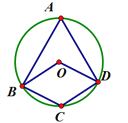
【題目】四邊形OBCD中的三個頂點在⊙O上,點A是⊙O上的一個動點(不與點B、C、D重合)。若四邊形OBCD是平行四邊形時,那么![]() 的數量關系是________________.
的數量關系是________________.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】等腰△ABC中,AB=AC,∠A=36°,D是AC上的一點,AD=BD,則以下結論中正確的有( )
①△BCD是等腰三角形;②點D是線段AC的黃金分割點;③△BCD∽△ABC;④BD平分∠ABC.
A. 1個 B. 2個 C. 3個 D. 4個
查看答案和解析>>
科目:初中數學 來源: 題型:
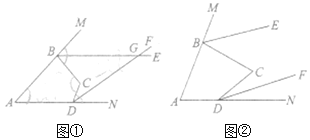
【題目】如圖①,![]() 、
、![]() 分別平分四邊形
分別平分四邊形![]() 的外角
的外角![]() 和
和![]() ,設
,設![]() ,
,![]() .
.
(1)若![]() ,則
,則![]()
![]() ;
;
(2)若![]() 與
與![]() 相交于點
相交于點![]() ,且
,且![]() ,求
,求![]() 、
、![]() 所滿足的等量關系式,并說明理由;
所滿足的等量關系式,并說明理由;
(3)如圖②,若![]() ,試判斷
,試判斷![]() 、
、![]() 的位置關系,并說明理由.
的位置關系,并說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
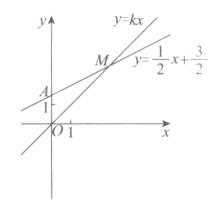
【題目】如圖,直線![]() 與y軸的交點為A,直線
與y軸的交點為A,直線![]() 與直線
與直線![]() 的交點M的坐標為
的交點M的坐標為![]() .
.
(1)求a和k的值;
(2)直接寫出關于x的不等式![]() 的解集;
的解集;
(3)若點B在x軸上,![]() ,直接寫出點B的坐標.
,直接寫出點B的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,在等腰直角三角形![]() 中,
中,![]() ,點
,點![]() 在
在![]() 邊上,連接
邊上,連接![]() ,連接
,連接![]()
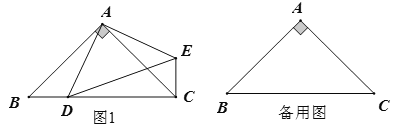
(1)求證:![]()
(2)點![]() 關于直線
關于直線![]() 的對稱點為
的對稱點為![]() ,連接
,連接![]()
①補全圖形并證明![]()
②利用備用圖進行畫圖、試驗、探究,找出當![]() 三點恰好共線時點
三點恰好共線時點![]() 的位置,請直接寫出此時
的位置,請直接寫出此時![]() 的度數,并畫出相應的圖形
的度數,并畫出相應的圖形
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在△ABC 中,AE、BF 是角平分線,交于 O 點.
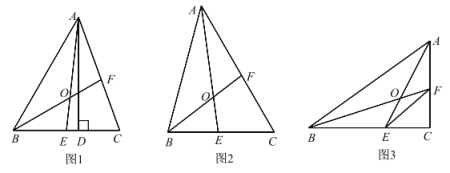
(1)如圖 1,AD 是高,∠BAC=90°,∠C=70°,求∠DAC 和∠BOA 的度數;
(2)如圖 2,若 OE=OF,求∠C 的度數;
(3)如圖 3,若∠C=90°,BC=8,AC=6,S△CEF=4,求 S△AOB.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com