Question

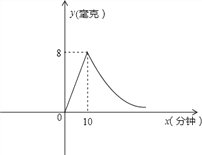
【題目】為預防甲型H1N1流感，某校對教室噴灑藥物進行消毒．已知噴灑藥物時每立方米空氣中的含藥量y（毫克）與時間x（分鐘）成正比，藥物噴灑完后，y與x成反比例（如圖所示）．現測得10分鐘噴灑完后，空氣中每立方米的含藥量為8毫克．

（1）求噴灑藥物時和噴灑完后，y關于x的函數關系式；

（2）若空氣中每立方米的含藥量低于2毫克學生方可進教室，問消毒開始后至少要經過多少分鐘，學生才能回到教室？

（3）如果空氣中每立方米的含藥量不低于4毫克，且持續時間不低于10分鐘時，才能殺滅流感病毒，那么此次消毒是否有效？為什么？

Answer 1

【答案】（1）①（0≤x＜10），②（x≥10）；（2）40分鐘；（3）本次消毒有效．

【解析】（1）分別設出噴灑藥物時和噴灑完后的函數解析式，代入點（10，8）即可求解．
（2）由（1）求得的反比例函數解析式，令y＜2，求得x的取值范圍即可．
（3）將y=4分別代入求得的正比例函數和反比例函數求得的x值作差與10比較即可得出此次消毒是否有效．

解：（1）①∵當0≤x＜10時y與x成正比例，

∴可設y=kx．

∵當x=10時，y=8，

∴8=10k．

∴k=．

∴（0≤x＜10）．

②∵當x≥10時y與x成反比例，

∴可設．

∵當x=10時，y=8，

∴．

∴k=80．

∴（x≥10）．

（2）當y＜2時，即．

解得x＞40．

∴消毒開始后至少要經過40分鐘，學生才能回到教室．

（3）將y=4代入中，得x=5；

將y=4代入中，得x=20；

∵20﹣5=15＞10，

∴本次消毒有效．