
【題目】某校一面墻![]() 前有一塊空地,校方準(zhǔn)備用長
前有一塊空地,校方準(zhǔn)備用長![]() 的柵欄(
的柵欄(![]() )圍成一個一面靠墻的長方形花圍,再將長方形
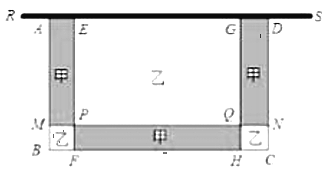
)圍成一個一面靠墻的長方形花圍,再將長方形![]() 分割成六塊(如圖所示) ,已知
分割成六塊(如圖所示) ,已知![]() ,
,![]() ,
,![]() ,設(shè)
,設(shè)![]() .
.
(1)用含![]() 的代數(shù)式表示:
的代數(shù)式表示:![]() ;
;![]() .
.
(2)當(dāng)長方形![]() 的面積等于
的面積等于![]() 時,求
時,求![]() 的長.
的長.
(3)若在如圖的甲區(qū)域種植花卉.乙區(qū)域種柏草坪,種柏花卉的成本為每平方米100元,種被草坪的成本為每平方米50元,若種植花卉與草坪的總費(fèi)用超過6300元,求花圍的寬![]() 的范圍.
的范圍.
【答案】(1)![]() ;(2)AB的長為
;(2)AB的長為![]() 或
或![]() ;(3)花圃的寬
;(3)花圃的寬![]() 時,總費(fèi)用超過 6300 元.
時,總費(fèi)用超過 6300 元.
【解析】
(1)根據(jù)矩形的性質(zhì)可得![]() ,根據(jù)柵欄的總長與矩形邊長的關(guān)系即可表示出
,根據(jù)柵欄的總長與矩形邊長的關(guān)系即可表示出![]() ,進(jìn)而表示出
,進(jìn)而表示出![]() ;
;
(2)先表示出長方形![]() 的邊長,利用長方形的面積公式列出方程,求解即可求得AB的長;
的邊長,利用長方形的面積公式列出方程,求解即可求得AB的長;
(3)先求出甲區(qū)域和乙區(qū)域的面積,設(shè)總費(fèi)用為![]() 元,依題意列出y關(guān)于x的關(guān)系式,利用二次函數(shù)的性質(zhì)求解不等式,即可求得花圍的寬
元,依題意列出y關(guān)于x的關(guān)系式,利用二次函數(shù)的性質(zhì)求解不等式,即可求得花圍的寬![]() 的范圍.
的范圍.
解:(1)∵四邊形![]() 是矩形,
是矩形,![]() ,
,
∴![]() ,
,
由題意得:![]() ,
,
∴![]() ,
,
∵![]() ,
,![]() ,則
,則![]() ,
,
∴四邊形![]() 是平行四邊形,
是平行四邊形,
∵![]() ,
,
∴四邊形![]() 是矩形,
是矩形,
∵![]() ,
,
∴四邊形![]() 是正方形,則
是正方形,則![]() ,
,
同理得:∴四邊形![]() 是正方形,則
是正方形,則![]() ,
,
∴![]() ,
,
故答案為:![]() ;
;![]() ;
;
(2)∵![]() ,
,
由題意可得:![]()
解得:![]() ,
,
![]() 的長為
的長為![]() 或
或![]() ;
;
(3)甲區(qū)域的面積![]() ,
,
乙區(qū)域的面積=![]() ,
,
設(shè)總費(fèi)用為![]() 元,由題意得:
元,由題意得:
![]() ,
,
整理得:![]() ,
,
令![]() ,即
,即![]() ,
,
解得:![]() ,
,
由二次函數(shù)的圖象與性質(zhì)可得:當(dāng) ![]() 時,
時,![]() ,
,
∴花圃的寬![]() 時,總費(fèi)用超過 6300 元.
時,總費(fèi)用超過 6300 元.
答:若種植花卉與草坪的總費(fèi)用超過6300元,花圍的寬![]() 的范圍為
的范圍為![]() .
.


 小學(xué)教材全測系列答案
小學(xué)教材全測系列答案 小學(xué)數(shù)學(xué)口算題卡脫口而出系列答案
小學(xué)數(shù)學(xué)口算題卡脫口而出系列答案
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,若干個全等的正五邊形排成環(huán)狀,圖中所示的是前3個正五邊形,要完成這一圓環(huán)還需正五邊形的個數(shù)為( )

A. 10 B. 9 C. 8 D. 7
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
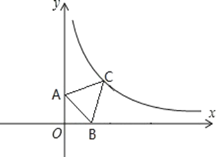
【題目】如圖所示,△ABC為等邊三角形,點(diǎn)A的坐標(biāo)為(0,4),點(diǎn)B在x軸上,點(diǎn)C在反比例函數(shù)![]() 的圖象上,則點(diǎn)B的坐標(biāo)為__________.
的圖象上,則點(diǎn)B的坐標(biāo)為__________.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】濟(jì)寧某校為了解九年級學(xué)生藝術(shù)測試情況.以九年極(1)班學(xué)生的藝術(shù)測試成績?yōu)闃颖荆?/span>![]() 、
、![]() 、
、![]() 、
、![]() 四個等級進(jìn)行統(tǒng)計,并將統(tǒng)計結(jié)果繪制成如下的統(tǒng)計圖,請你結(jié)合圖中所給信息解答下列問題:
四個等級進(jìn)行統(tǒng)計,并將統(tǒng)計結(jié)果繪制成如下的統(tǒng)計圖,請你結(jié)合圖中所給信息解答下列問題:

(說明:![]() 級:90分~100分;
級:90分~100分;![]() 級:75分~89分;
級:75分~89分;![]() 級60分~74分;
級60分~74分;![]() 級:60分以下)
級:60分以下)
(1)此次抽樣共調(diào)查了多少名學(xué)生?
(2)請求出樣本中![]() 級的學(xué)生人數(shù),井補(bǔ)全條形統(tǒng)計圖;
級的學(xué)生人數(shù),井補(bǔ)全條形統(tǒng)計圖;
(3)若該校九年級有1000名學(xué)生,請你用此樣本估計藝術(shù)測試中分?jǐn)?shù)不低于75分的學(xué)生人數(shù),
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
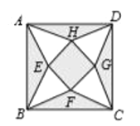
【題目】將一個邊長為4的正方形![]() 分割成如圖所示的9部分,其中
分割成如圖所示的9部分,其中![]() ,
,![]() ,
,![]() ,
,![]() 全等,
全等,![]() ,
,![]() ,
,![]() ,
,![]() 也全等,中間小正方形
也全等,中間小正方形![]() 的面積與
的面積與![]() 面積相等,且
面積相等,且![]() 是以
是以![]() 為底的等腰三角形,則
為底的等腰三角形,則![]() 的面積為( )
的面積為( )
A.2B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
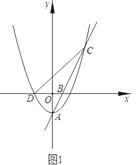
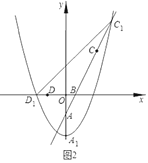
【題目】如圖1,拋物線![]() 的頂點(diǎn)為點(diǎn)
的頂點(diǎn)為點(diǎn)![]() ,與
,與![]() 軸的負(fù)半軸交于點(diǎn)
軸的負(fù)半軸交于點(diǎn)![]() ,直線
,直線![]() 交拋物線W于另一點(diǎn)
交拋物線W于另一點(diǎn)![]() ,點(diǎn)
,點(diǎn)![]() 的坐標(biāo)為
的坐標(biāo)為![]() .
.
(1)求直線![]() 的解析式;
的解析式;
(2)過點(diǎn)![]() 作
作![]() 軸,交
軸,交![]() 軸于點(diǎn)
軸于點(diǎn)![]() ,若
,若![]() 平分
平分![]() ,求拋物線W的解析式;
,求拋物線W的解析式;
(3)若![]() ,將拋物線W向下平移
,將拋物線W向下平移![]() 個單位得到拋物線
個單位得到拋物線![]() ,如圖2,記拋物線
,如圖2,記拋物線![]() 的頂點(diǎn)為
的頂點(diǎn)為![]() ,與
,與![]() 軸負(fù)半軸的交點(diǎn)為
軸負(fù)半軸的交點(diǎn)為![]() ,與射線
,與射線![]() 的交點(diǎn)為
的交點(diǎn)為![]() .問:在平移的過程中,
.問:在平移的過程中,![]() 是否恒為定值?若是,請求出
是否恒為定值?若是,請求出![]() 的值;若不是,請說明理由.
的值;若不是,請說明理由.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】拋物線![]() (
(![]() 為常數(shù))與
為常數(shù))與![]() 軸交于點(diǎn)
軸交于點(diǎn)![]() 和
和![]() 與
與![]() 軸交于點(diǎn)
軸交于點(diǎn)![]() ,點(diǎn)
,點(diǎn)![]() 為拋物線頂點(diǎn).
為拋物線頂點(diǎn).
(Ⅰ)當(dāng)![]() 時,求點(diǎn)
時,求點(diǎn)![]() ,點(diǎn)
,點(diǎn)![]() 的坐標(biāo);
的坐標(biāo);
(Ⅱ)①若頂點(diǎn)![]() 在直線
在直線![]() 上時,用含有
上時,用含有![]() 的代數(shù)式表示
的代數(shù)式表示![]() ;
;
②在①的前提下,當(dāng)點(diǎn)![]() 的位置最高時,求拋物線的解析式;
的位置最高時,求拋物線的解析式;
(Ⅲ)若![]() ,當(dāng)
,當(dāng)![]() 滿足
滿足![]() 值最小時,求
值最小時,求![]() 的值.
的值.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】在平面直角坐標(biāo)系xOy中,將拋物線y=﹣x2平移后經(jīng)過點(diǎn)A(﹣1,0)、B(4,0),且平移后的拋物線與y軸交于點(diǎn)C(如圖).
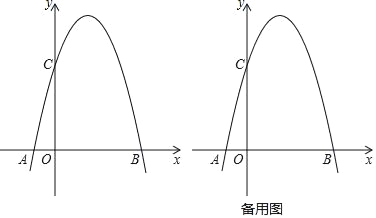
(1)求平移后的拋物線的表達(dá)式;
(2)如果點(diǎn)D在線段CB上,且CD=![]() ,求∠CAD的正弦值;
,求∠CAD的正弦值;
(3)點(diǎn)E在y軸上且位于點(diǎn)C的上方,點(diǎn)P在直線BC上,點(diǎn)Q在平移后的拋物線上,如果四邊形ECPQ是菱形,求點(diǎn)Q的坐標(biāo).
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】為了從小華和小亮兩人中選拔一人參加射擊比賽,現(xiàn)對他們的射擊水平進(jìn)行測試,兩人在相同條件下各射擊6次,命中的環(huán)數(shù)如下(單位:環(huán)):
小華:7,8,7,8,9,9; 小亮:5,8,7,8,10,10.
(1)填寫下表:
平均數(shù)(環(huán)) | 中位數(shù)(環(huán)) | 方差(環(huán)2) | |
小華 | 8 | ||
小亮 | 8 | 3 |
(2)根據(jù)以上信息,你認(rèn)為教練會選擇誰參加比賽,理由是什么?
(3)若小亮再射擊2次,分別命中7環(huán)和9環(huán),則小亮這8次射擊成績的方差 .(填“變大”、“變小”、“不變”)
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com