
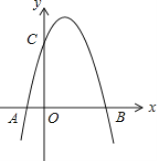
【題目】如圖,二次函數![]() 的圖象與x軸的一個交點為
的圖象與x軸的一個交點為![]() ,另一個交點為A,且與y軸相交于C點
,另一個交點為A,且與y軸相交于C點
(1)求m的值及C點坐標;
(2)在直線BC上方的拋物線上是否存在一點M,使得它與B,C兩點構成的三角形面積最大,若存在,求出此時M點坐標;若不存在,請簡要說明理由
(3)P為拋物線上一點,它關于直線BC的對稱點為Q,當四邊形PBQC為菱形時,求點P的坐標(直接寫出答案);
【答案】(1)![]()
![]()
(2) 存在, ![]()
(3)![]() 點坐標為(
點坐標為(![]() )或(
)或(![]() )
)
【解析】
![]() 將點
將點![]() 坐標代入得到
坐標代入得到![]() 的值,再令
的值,再令![]() 得到
得到![]() 點坐標;
點坐標;
![]() 點在直線
點在直線![]() 上方的拋物線上,要使
上方的拋物線上,要使![]() 面積最大,則
面積最大,則![]() 點的位置應在拋物線上且離直線的距離最遠處,把直線
點的位置應在拋物線上且離直線的距離最遠處,把直線![]() 向上平移和拋物線只有一個公共點時,此時的交點即為
向上平移和拋物線只有一個公共點時,此時的交點即為![]() 點的位置,然后根據二次函數的性質,求出
點的位置,然后根據二次函數的性質,求出![]() 值和
值和![]() 點坐標.
點坐標.
![]() 連接
連接![]() 交
交![]() 于點
于點![]() ,根據菱形的性質得到幾何關系,用中點坐標公式和系數與直線位置的特殊關系,確定
,根據菱形的性質得到幾何關系,用中點坐標公式和系數與直線位置的特殊關系,確定![]() 點坐標并求出直線
點坐標并求出直線![]() 的解析式,聯立直線
的解析式,聯立直線![]() 的解析式與拋物線解析式,即可求出
的解析式與拋物線解析式,即可求出![]() 點坐標.
點坐標.
解:![]() 將點
將點![]() 的坐標代入二次函數
的坐標代入二次函數![]() ,即
,即![]() ,解得
,解得![]() ,故二次函數解析式為
,故二次函數解析式為![]() ,令
,令![]() ,解得
,解得![]() ,故
,故![]() 點坐標為
點坐標為![]() ;
;
(2)存在,
理由:![]() ,
,![]()
![]() 直線
直線![]() 的解析式為
的解析式為![]() ,
,
當直線![]() 向上平移
向上平移![]() 單位后和拋物線只有一個公共點時,
單位后和拋物線只有一個公共點時,![]() 面積最大,
面積最大,
![]()
整理得:![]()
![]() ,
,
![]()
![]()
![]()
![]()
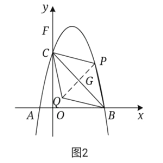
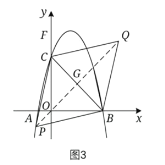
如圖2、圖3所示,連接![]() 交
交![]() 于點
于點![]() 。
。
因為四邊形![]() 是菱形,所以
是菱形,所以![]() 為
為![]() 的中點,
的中點,
因為點![]() 的坐標分別為
的坐標分別為![]() 、
、![]() ,所以由中點坐標公式得
,所以由中點坐標公式得![]() 點坐標為
點坐標為![]() ,
,
由(2)可知直線![]() 的解析式為
的解析式為![]() ,
,
由于![]() ,所以設直線
,所以設直線![]() 的解析式為
的解析式為![]() ,
,
將![]() 代入,求得直線
代入,求得直線![]() 的解析式為
的解析式為![]() ,
,
將直線![]() 的解析式與拋物線解析式聯立得:
的解析式與拋物線解析式聯立得:
![]() ,消去
,消去![]() 得:
得:![]() ,
,
解得:![]() ,
,
將![]() 代入直線
代入直線![]() 的解析式得
的解析式得![]() ,
,
將![]() 代入直線
代入直線![]() 的解析式得
的解析式得![]() ,
,
故當四邊形![]() 為菱形時,
為菱形時,![]() 點坐標為(
點坐標為(![]() )或(
)或(![]() ).
).


 輕松課堂單元期中期末專題沖刺100分系列答案
輕松課堂單元期中期末專題沖刺100分系列答案科目:初中數學 來源: 題型:
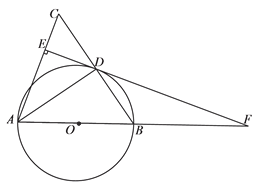
【題目】如圖,在△ABC中,AB=AC,以AB為直徑作半圓O,交BC于點D,連接AD,過點D作DE⊥AC,垂足為點E,交AB的延長線于點F.
(1)求證:EF是⊙O的切線.
(2)如果⊙O的半徑為5,sin∠ADE=![]() ,求BF的長.
,求BF的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在一斜坡坡頂![]() 處的同一水平線上有一古塔,為測量塔高
處的同一水平線上有一古塔,為測量塔高![]() ,數學老師帶領同學在坡腳
,數學老師帶領同學在坡腳![]() 處測得斜坡的坡角為
處測得斜坡的坡角為![]() ,且
,且![]() ,塔頂
,塔頂![]() 處的仰角為
處的仰角為![]() ,他們沿著斜坡攀行了
,他們沿著斜坡攀行了![]() 米,到達坡頂
米,到達坡頂![]() 處,在
處,在![]() 處測得塔頂
處測得塔頂![]() 的仰角為
的仰角為![]() .
.
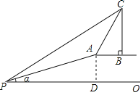
(1)求斜坡的高度![]() ;
;
(2)求塔高![]() .
.
查看答案和解析>>
科目:初中數學 來源: 題型:
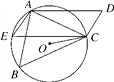
【題目】如圖,在四邊形ABCD中,AD=BC,∠B=∠D,AD不平行于BC,過點C作CE∥AD交△ABC的外接圓O于點E,連接AE.
(1)求證:四邊形AECD為平行四邊形;
(2)連接CO,求證:CO平分∠BCE.
查看答案和解析>>
科目:初中數學 來源: 題型:
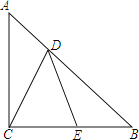
【題目】△ABC中,AC=BC,∠ACB=90°,點D在AB上,點E在BC上,且AD=BE,BD=AC,連DE、CD.
(1)找出圖中全等圖形,并證明;
(2)求∠ACD的度數;
查看答案和解析>>
科目:初中數學 來源: 題型:
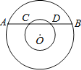
【題目】如圖,兩同心圓中,大圓的弦![]() 交小圓于
交小圓于![]() 、
、![]() 兩點,點
兩點,點![]() 到
到![]() 的距離等于
的距離等于![]() 的一半,且
的一半,且![]() .則大小圓的半徑之比為( )
.則大小圓的半徑之比為( )
A. ![]() :1 B. 2:
:1 B. 2:![]() C. 10:
C. 10:![]() D. 3:1
D. 3:1
查看答案和解析>>
科目:初中數學 來源: 題型:
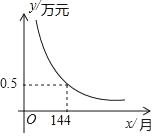
【題目】為了方便孩子入學,小王家購買了一套學區房,交首付款15萬元,剩余部分向銀行貸款,貸款及貸款利息按月分期還款,每月還款數相同.計劃每月還款y萬元,x個月還清貸款,若y是x的反比例函數,其圖象如圖所示:
(1)求y與x的函數解析式;
(2)若小王家計劃180個月(15年)還清貸款,則每月應還款多少萬元?
查看答案和解析>>
科目:初中數學 來源: 題型:
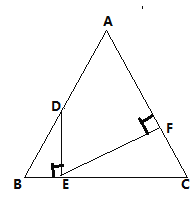
【題目】如圖,等邊△ABC的邊長為12, D為AB邊上一動點,過點D作DE⊥BC于點E.過點E作EF⊥AC于點F.
(1)若AD=2,求AF的長;
(2)當AD取何值時,DE=EF?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com