
【題目】如圖,在![]() 中,
中,![]() ,
,![]() 是過點
是過點![]() 的直線,
的直線,![]() 于
于![]() ,
,![]() 于點
于點![]() ;
;
(1)若![]() 、
、![]() 在
在![]() 的同側(如圖所示)且
的同側(如圖所示)且![]() .求證:
.求證:![]() ;
;
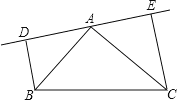
(2)若![]() 、
、![]() 在
在![]() 的兩側(如圖所示),且
的兩側(如圖所示),且![]() ,其他條件不變,
,其他條件不變,![]() 與
與![]() 仍垂直嗎?若是請給出證明;若不是,請說明理由.
仍垂直嗎?若是請給出證明;若不是,請說明理由.
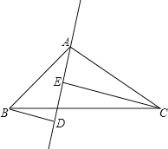
【答案】(1)見解析;(2)見解析.
【解析】
(1)由已知條件,證明ABD≌△CAE,再利用角與角之間的關系求證∠BAD+∠CAE=90°,即可證明AB⊥AC;
(2)同(1),先證ABD≌△CAE,再利用角與角之間的關系求證∠BAD+∠CAE=90°,即可證明AB⊥AC.
(1)證明:∵BD⊥DE,CE⊥DE,
∴∠ADB=∠ABC=∠90,
在Rt△ABD和Rt△CAE中,∵![]() ,
,
∴Rt△ABD≌Rt△CAE.
∴∠DAB=∠ECA,∠DBA=∠ACE.
∵∠DAB+∠DBA=90,∠EAC+∠ACE=90,
∴∠BAD+∠CAE=90.
∠BAC=180-(∠BAD+∠CAE)=90.
∴AB⊥AC.
(2)AB⊥AC.理由如下:
同(1)一樣可證得Rt△ABD=Rt△ACE.
∴∠DAB=∠ECA,∠DBA=∠EAC,
∵∠CAE+∠ECA=90°,
∴∠CAE+∠BAD=90,即∠BAC=90°,
∴AB⊥AC.



 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:初中數學 來源: 題型:
【題目】已知△ABC中,AB=AC,∠BAC=120°,在BC上取一點O,以O為圓心、OB為半徑作圓,且⊙O過A點. 如圖①,若⊙O的半徑為5,求線段OC的長;
如圖②,過點A作AD∥BC交⊙O于點D,連接BD,求 ![]() 的值.
的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為宣傳節約用水,小明隨機調查了某小區部分家庭5月份的用水情況,并將收集的數據整理成如圖所示的統計圖.
(1)小明一共調查了多少戶家庭?
(2)求所調查家庭5月份用水量的眾數、平均數.
(3)若該小區有400戶居民,請你估計這個小區5月份的用水量.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖:在△ABC中,AC=BC,D是AB上的一點,AE⊥CD于點E,BF⊥CD于點F,若CE=BF,AE=EF+BF.試判斷AC與BC的位置關系,并說明理由.
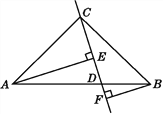
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知甲同學手中藏有三張分別標有數字 ![]() 、
、 ![]() 、1的卡片,乙同學手中藏有三張分別標有數字1、3、2的卡片,卡片外形相同.現從甲乙兩人手中各任取一張卡片,并將它們的數字分別記為a,b.
、1的卡片,乙同學手中藏有三張分別標有數字1、3、2的卡片,卡片外形相同.現從甲乙兩人手中各任取一張卡片,并將它們的數字分別記為a,b.
(1)請你用樹形圖或列表法列出所有可能的結果;
(2)現制定一個游戲規則:若所選出的a,b能使得ax2+bx+1=0有兩個不相等的實數根,則甲獲勝;否則乙獲勝.請問這樣的游戲規則公平嗎?請用概率知識解釋.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】我市某中學七、八年級各選派10名選手參加學校舉辦的“愛我荊門”知識競賽,計分采用10分制,選手得分均為整數,成績達到6分或6分以上為合格,達到9分或10分為優秀.這次競賽后,七、八年級兩支代表隊選手成績分布的條形統計圖和成績統計分析表如下,其中七年級代表隊得6分、10分的選手人數分別為a,b.
隊別 | 平均分 | 中位數 | 方差 | 合格率 | 優秀率 |
七年級 | 6.7 | m | 3.41 | 90% | n |
八年級 | 7.1 | 7.5 | 1.69 | 80% | 10% |
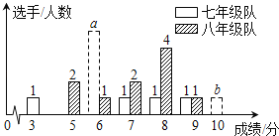
(1)請依據圖表中的數據,求a,b的值;
(2)直接寫出表中的m,n的值;
(3)有人說七年級的合格率、優秀率均高于八年級,所以七年級隊成績比八年級隊好,但也有人說八年級隊成績比七年級隊好.請你給出兩條支持八年級隊成績好的理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如果一個三角形能被一條線段分割成兩個等腰三角形,那么稱這條線段為這個三角形的特異線,稱這個三角形為特異三角形.
(1)如圖1,△ABC中,∠B=2∠C,線段AC的垂直平分線交AC于點D,交BC于點E.求證:AE是△ABC的一條特異線.
(2)如圖2,已知△ABC是特異三角形,且∠A=30°,∠B為鈍角,求出所有可能的∠B的度數.
(3)如圖3,△ABC是一個腰長為2的等腰銳角三角形,且它是特異三角形,若它的頂角度數為整數,請求出其特異線的長度;若它的頂角度數不是整數,請直接寫出頂角度數.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com