
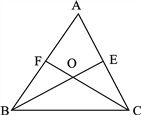
【題目】如圖:三角形![]() 中,
中,![]() 、
、![]() 分別是
分別是![]() 和
和![]() 的平分線,
的平分線,![]() 、
、![]() 相交于點
相交于點![]() (知識鏈接:三角形三個內角的和是180°。如圖
(知識鏈接:三角形三個內角的和是180°。如圖![]() 是三角形
是三角形![]() 的一個內角)
的一個內角)
(1)如果![]() °求
°求![]() 的度數。
的度數。
(2)如果![]() °直接寫出
°直接寫出![]() 的度數
的度數
(3)探求![]() 和
和![]() 的關系(用等式表示),并簡要說明理由。
的關系(用等式表示),并簡要說明理由。
【答案】(1)![]() 的度數為110°;
的度數為110°;
(2)![]() 的度數為115°;
的度數為115°;
(3)∠BOC=90°+![]() ∠A,理由見解析.
∠A,理由見解析.
【解析】
(1)先根據三角形內角和定理求出∠ABC+∠ACB的度數,再根據角平分線的性質可求出∠EBC+∠FCB的度數,再由三角形的內角和為180°即可解答;
(2)同(1),根據三角形的內角和定理及角平分線的性質解答即可;
(3)根據(1)的敘述寫出結論即可.
解:(1)∵∠A+∠ABC+∠ACB=180°,∠A=40°,
∴∠ABC+∠ACB=180°-∠A=140°,
∵∠EBC=![]() ∠ABC∠FCB=
∠ABC∠FCB=![]() ∠ACB,
∠ACB,
∴∠EBC+∠FCB=![]() (∠ABC+∠ACB)=70°,
(∠ABC+∠ACB)=70°,
∴∠BOC=180°-70°=110°;
(2)同(1)∠BOC=180°-![]() =180°-
=180°-![]() =115°;
=115°;
(3)由(1)可知:∠BOC=90°+![]() ∠A,
∠A,
理由同(1),∵∠A+∠ABC+∠ACB=180°,BE、CF分別是∠ABC、∠ACB的平分線,
∴∠OBC=![]() ∠ABC,∠OCB=
∠ABC,∠OCB=![]() ∠ACB,
∠ACB,
∴∠OBC+∠OCB=![]() (∠ABC+∠ACB),
(∠ABC+∠ACB),
∴∠OBC+∠OCB=![]() (180°-∠A)=90°-
(180°-∠A)=90°-![]() ∠A,
∠A,
∵∠BOC+∠OBC+∠OCB=180°,
∴∠BOC=180°-(∠OBC+∠OCB)=180°-90°+![]() ∠A=90°+
∠A=90°+![]() ∠A.
∠A.
“點睛”本題考查的是三角形內角和定理及角平分線的性質,比較簡單.


科目:初中數學 來源: 題型:
【題目】![]() 為直線
為直線![]() 上一點,以
上一點,以![]() 為頂點作
為頂點作![]() ,射線
,射線![]() 平分
平分![]() .
.
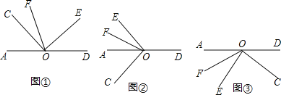
![]() 如圖①,
如圖①,![]() 與
與![]() 的數量關系為________,
的數量關系為________,![]() 和
和![]() 的數量關系為_________;
的數量關系為_________;
![]() 若將
若將![]() 繞點
繞點![]() 旋轉至圖②的位置,
旋轉至圖②的位置,![]() 依然平分
依然平分![]() ,請寫出
,請寫出![]() 和
和![]() 之間的數量關系,并說明理由;
之間的數量關系,并說明理由;
![]() 若將
若將![]() 繞點
繞點![]() 旋轉至圖③的位置,射線
旋轉至圖③的位置,射線![]() 依然平分
依然平分![]() ,請直接寫出
,請直接寫出![]() 和
和![]() 之間的數量關系.
之間的數量關系.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知二次函數y=x2﹣x+a(a>0),當自變量x取p時的函數值小于0,那么當自變量x取p﹣1時的函數值( )
A.小于0
B.大于0
C.等于0
D.與0的大小關系不確定
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知△ABC中,AB=AC,點D在底邊BC上,添加下列條件后,仍無法判定△ABD≌△ACD的是( )

A. BD=CD B. ∠BAD=∠CAD C. ∠B=∠C D. ∠ADB=∠ADC
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知線段MN=3cm,在線段MN上取一點P,使PM=PN;延長線段MN到點A,使AN=![]() MN;延長線段NM到點B,使BN=3BM.
MN;延長線段NM到點B,使BN=3BM.
(1)根據題意,畫出圖形;
(2)求線段AB的長;
(3)試說明點P是哪些線段的中點.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com