Question

已知頂點為A(1,5)的拋物線經過點B(5,1).

(1)求拋物線的解析式;

(2)如圖（1）,設C,D分別是軸、軸上的兩個動點，求四邊形ABCD周長的最小值；

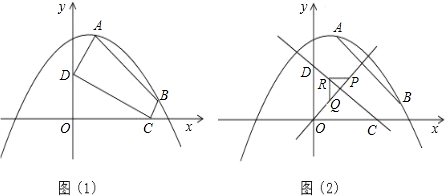
（3）在（2）中，當四邊形ABCD的周長最小時，作直線CD.設點P()()是直線上的一個動點，Q是OP的中點，以PQ為斜邊按圖（2）所示構造等腰直角三角形PRQ.

①當△PBR與直線CD有公共點時,求的取值范圍；

②在①的條件下，記△PBR與△COD的公共部分的面積為S.求S關于的函數關系式，并求S的最大值。

 

 

 

Answer 1

解：（1）∵拋物線的頂點為A（1，5），

∴設拋物線的解析式為，

將點B（5，1）代入，得，

解得，

∴

（2）作A關于y軸的對稱點，作B關于x軸的對稱點，顯然，

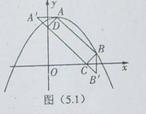如圖(5.1)，連結分別交x軸、y軸于C、D兩點，

∵，

∴此時四邊形ABCD的周長最小，最小值就是。

而，

∴

四邊形ABCD周長的的最小值為。

（3）①點B關于x軸的對稱點B′（），點A關于y軸的對稱點A′（﹣1，5），連接A′B′，與x軸，y軸交于C，D點，

∴CD的解析式為：，

聯立，

得：

∵點P在上，點Q是OP的中點，

∴要使等腰直角三角形與直線CD有公共點，則．

故的取值范圍是：．

 

②如圖：

點E（2，2），當EP=EQ時，，得：，

當時，

當時，．

當時，

當時，．

故的最大值為：．

解析:略