
【題目】在平面直角坐標(biāo)系中,拋物線y=﹣![]() x2+x+2
x2+x+2![]() 與x軸交于A,B兩點(diǎn),交y軸于點(diǎn)C,點(diǎn)C關(guān)于拋物線對(duì)稱(chēng)軸對(duì)稱(chēng)的點(diǎn)為D.
與x軸交于A,B兩點(diǎn),交y軸于點(diǎn)C,點(diǎn)C關(guān)于拋物線對(duì)稱(chēng)軸對(duì)稱(chēng)的點(diǎn)為D.
(1)求點(diǎn)D的坐標(biāo)及直線AD的解析式;
(2)如圖1,連接CD、AD、BD,點(diǎn)M為線段CD上一動(dòng)點(diǎn),過(guò)M作MN∥BD交線段AD于N點(diǎn),點(diǎn)P是y軸上的動(dòng)點(diǎn),當(dāng)△CMN的面積最大時(shí),求△MPN的周長(zhǎng)取得最小值時(shí)點(diǎn)P的坐標(biāo);
(3)如圖2,線段AE在第一象限內(nèi)交BD于點(diǎn)E,其中tan∠EAB=![]() ,將拋物線向右水平移動(dòng),點(diǎn)A平移后的對(duì)應(yīng)點(diǎn)為點(diǎn)G;將△ABD繞點(diǎn)B逆時(shí)針旋轉(zhuǎn),旋轉(zhuǎn)后的三角形紀(jì)為△A1BD1,若射線BD1與線段AE的交點(diǎn)為F,連接FG.若線段FG把△ABF分成△AFG和△BFG兩個(gè)三角形,是否存在點(diǎn)G,使得△AFG是直角三角形且△BFG是等腰三角形?若存在,請(qǐng)直接寫(xiě)出點(diǎn)G的坐標(biāo);若不存在,請(qǐng)說(shuō)明理由.
,將拋物線向右水平移動(dòng),點(diǎn)A平移后的對(duì)應(yīng)點(diǎn)為點(diǎn)G;將△ABD繞點(diǎn)B逆時(shí)針旋轉(zhuǎn),旋轉(zhuǎn)后的三角形紀(jì)為△A1BD1,若射線BD1與線段AE的交點(diǎn)為F,連接FG.若線段FG把△ABF分成△AFG和△BFG兩個(gè)三角形,是否存在點(diǎn)G,使得△AFG是直角三角形且△BFG是等腰三角形?若存在,請(qǐng)直接寫(xiě)出點(diǎn)G的坐標(biāo);若不存在,請(qǐng)說(shuō)明理由.

【答案】(1)D(![]() ,2
,2![]() );直線AD解析式y=x+
);直線AD解析式y=x+![]() ;(2)P(0,
;(2)P(0,![]() );(3)G(
);(3)G(![]() ,0),(
,0),(![]() ,0),(
,0),(![]() ,0).
,0).
【解析】
(1)根據(jù)題意可得A,B,C坐標(biāo),根據(jù)對(duì)稱(chēng)可求D點(diǎn)坐標(biāo),用待定系數(shù)法可求AD解析式;(2)作DH⊥AB,MT⊥AB,交AD于T,作NK⊥MT,設(shè)M(m,2![]() ),則T(m,m+
),則T(m,m+![]() ),根據(jù)相似三角形可得MK=
),根據(jù)相似三角形可得MK=![]() MT,用m表示△CMN的面積,根據(jù)二次函數(shù)的最值問(wèn)題,可求M點(diǎn)坐標(biāo),作M關(guān)于y軸對(duì)稱(chēng)點(diǎn)M1(-
MT,用m表示△CMN的面積,根據(jù)二次函數(shù)的最值問(wèn)題,可求M點(diǎn)坐標(biāo),作M關(guān)于y軸對(duì)稱(chēng)點(diǎn)M1(-![]() ,2
,2![]() ),連接M1N交y軸于點(diǎn)P,利用待定系數(shù)法確定函數(shù)關(guān)系式以及直線與坐標(biāo)軸的交點(diǎn)的求法求得點(diǎn)P的坐標(biāo);(3)如圖3,4,5,分類(lèi)討論,通過(guò)數(shù)量關(guān)系列出方程,可求G點(diǎn)坐標(biāo).
),連接M1N交y軸于點(diǎn)P,利用待定系數(shù)法確定函數(shù)關(guān)系式以及直線與坐標(biāo)軸的交點(diǎn)的求法求得點(diǎn)P的坐標(biāo);(3)如圖3,4,5,分類(lèi)討論,通過(guò)數(shù)量關(guān)系列出方程,可求G點(diǎn)坐標(biāo).
(1)令x=0,則y=2![]() ,
,
∴C(0,2![]() ),
),
∵對(duì)稱(chēng)軸為x=![]() ,且C,D關(guān)于對(duì)稱(chēng)軸對(duì)稱(chēng),
,且C,D關(guān)于對(duì)稱(chēng)軸對(duì)稱(chēng),
∴D(![]() ,2
,2![]() ).
).
令y=0,則0=﹣![]() x2+x+2
x2+x+2![]() ,
,
∴x1=﹣![]() ,x2=2
,x2=2![]() ,
,
∴A(﹣![]() ,0),B(2
,0),B(2![]() ,0),
,0),
設(shè)直線AD解析式y=kx+b,
![]() ,
,
解得:k=1,b=![]() ,
,
∴直線AD解析式y=x+![]() ;
;
(2)如圖1:作DH⊥AB,MT⊥AB,交AD于T,作NK⊥MT
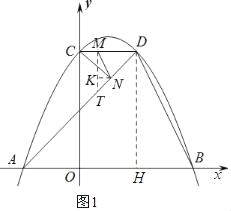
設(shè)M(m,2![]() ),則T(m,m+
),則T(m,m+![]() )
)
∵A(﹣![]() ,0),D(
,0),D(![]() ,2
,2![]() ),
),
∴AH=DH
∴∠DAH=∠ADH=45°=∠CDA
∵MT∥DH,KN∥CD
∴∠KNT=∠KTN=45°=∠CDA
∴KT=KN,MT=MD
∵MN∥BD,
∴∠MND=∠ADB且∠CDA=∠DAB
∴△ADB∽△MND,
∴![]() ,
,
∴ND=![]() MD.
MD.
∵DT=![]() MD,
MD,
∴NT=![]() MD.
MD.
∵KN∥CD,
∴![]() ,
,
∴KT=![]() MT
MT
∴KM=![]() MT=
MT=![]() (
(![]() ﹣m)
﹣m)
∴S△CMN=![]() CM×KM=
CM×KM=![]() m×
m×![]() (
(![]() ﹣m)=﹣
﹣m)=﹣![]() m2+
m2+![]() m
m
∴當(dāng)m=![]() 時(shí),S△CMN最大值.
時(shí),S△CMN最大值.
∴M(![]() ,2
,2![]() ).
).
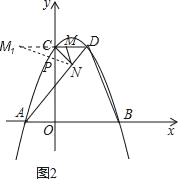
如圖2 作M關(guān)于y軸對(duì)稱(chēng)點(diǎn)M1(﹣![]() ,2
,2![]() ),
),
由B(2![]() ,0),D(
,0),D(![]() ,2
,2![]() )得到直線BD的解析式為:y=﹣2x+4
)得到直線BD的解析式為:y=﹣2x+4![]() .
.
∵MN∥BD,
∴設(shè)直線MN的解析式為:y=﹣x+t.
把M(![]() ,2
,2![]() )代入求得:y=﹣x+
)代入求得:y=﹣x+![]() .
.
聯(lián)立方程組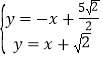 ,
,
解之得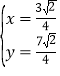 ,即N(
,即N(![]() ),
),
由M1(﹣![]() ,2
,2![]() ),N(
),N(![]() )得到直線M1N的解析式為:y=﹣
)得到直線M1N的解析式為:y=﹣![]() x+
x+![]() .
.
令x=0,則y=![]() ,即:P(0,
,即:P(0,![]() ).
).
(3)如圖3:

①當(dāng)AG=FG,∠GFB=90°時(shí),∵tan∠EAB=![]() ,
,
∴設(shè)FH=a,則AH=2a,設(shè)AG=FG=x,則GH=2a﹣x
∵FH2+GH2=FG2
∴a2+(2a﹣x)2=x2
∴x=![]() a,
a,
∴GH=![]() a,
a,
∵FH⊥AB,GF⊥FB
∴∠FBG=∠GFH
∴tan∠GFH=tan∠FBG
∴![]() ,
,
∴BH=![]() a
a
∵AH+BH=AB=3![]() ,
,
∴2a+![]() a=3
a=3![]() ,
,
∴a=![]() ,
,
∵OG=AG﹣AO
∴OG=![]() ×
×![]() ﹣
﹣![]() =
=![]() ,
,
∴G(![]() ,0)
,0)
②如圖4
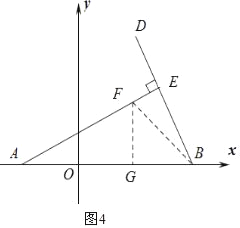
當(dāng)FG=BG,∠AGF=90°時(shí),設(shè)GF=a,則AG=2a,BG=a,
∴AB=AG+BG=3a=3![]() ,
,
∴a=![]() ,
,
∴G(![]() ,0);
,0);
③如圖5:
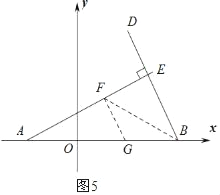
當(dāng)FG=BG,∠AFG=90°時(shí),設(shè)GF=a,則BG=a,AG=![]() a.
a.
∴AB=AG+BG=![]() a+a=3
a+a=3![]() ,
,
∴a=![]() ,
,
∵OG=AG﹣AO=![]() a﹣
a﹣![]() =
=![]() ,
,
∴G(![]() ,0),
,0),
綜上所述G(![]() ,0),(
,0),(![]() ,0),(
,0),(![]() ,0).
,0).



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來(lái)源: 題型:
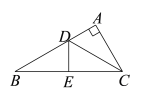
【題目】如圖,在△ABC中,∠A=90°,CD是∠ACB的平分線, DE垂直平分BC,若DE=2,則AB=___________.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
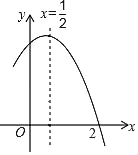
【題目】如圖是二次函數(shù)y=ax2+bx+c(a≠0)圖象的一部分,對(duì)稱(chēng)軸為x=![]() ,且經(jīng)過(guò)點(diǎn)(2,0),下列說(shuō)法:①abc<0;②﹣2b+c=0;③4a+2b+c<0;④若(
,且經(jīng)過(guò)點(diǎn)(2,0),下列說(shuō)法:①abc<0;②﹣2b+c=0;③4a+2b+c<0;④若(![]() ,y1)、(
,y1)、(![]() ,y2)是拋物線上的兩點(diǎn),則y1<y2;⑤
,y2)是拋物線上的兩點(diǎn),則y1<y2;⑤![]() >m(am+b)(其中m≠
>m(am+b)(其中m≠![]() ).其中說(shuō)法正確的是_____
).其中說(shuō)法正確的是_____
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】某科研小組獲取了聲音在空氣中傳播的速度v與空氣溫度t關(guān)系的一些數(shù)據(jù)如下表:
溫度t(°C) | -20 | -10 | 0 | 10 | 20 | 30 |
聲速v(m/s) | 318 | 324 | 330 | 336 | 342 | 348 |
(1)根據(jù)表中提供的信息,可推測(cè)速度v是溫度t的一次函數(shù),請(qǐng)你寫(xiě)出其函數(shù)表達(dá)式;
(2)當(dāng)空氣溫度為25°C,聲音10秒可以傳播多少米?
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】直線y=2x+3與拋物線y=ax2交于A、B兩點(diǎn),已知點(diǎn)A的橫坐標(biāo)為3.
(1)求A、B兩點(diǎn)的坐標(biāo)及拋物線的解析式;
(2)O為坐標(biāo)原點(diǎn),求△AOB的面積.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知邊長(zhǎng)為2的正六邊形ABCDEF在平面直角坐標(biāo)系中的位置如圖所示,點(diǎn)B在原點(diǎn),把正六邊形ABCDEF沿x軸正半軸作無(wú)滑動(dòng)的連續(xù)翻轉(zhuǎn),每次翻轉(zhuǎn)60°,經(jīng)過(guò)2018次翻轉(zhuǎn)之后,點(diǎn)B的坐標(biāo)是______.
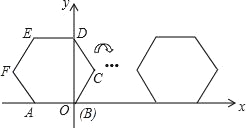
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,在![]() 中,
中,![]() 和
和![]() 的平分線相交于點(diǎn)
的平分線相交于點(diǎn)![]() ,過(guò)
,過(guò)![]() 作
作![]() ,交
,交![]() 于點(diǎn)
于點(diǎn)![]() ,交
,交![]() 于點(diǎn)
于點(diǎn)![]() .若
.若![]() ,則線段
,則線段![]() 的長(zhǎng)為______.
的長(zhǎng)為______.
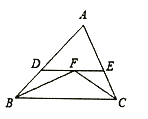
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,邊長(zhǎng)為![]() 的正方形
的正方形![]() 中,
中,![]() 為
為![]() 的中點(diǎn),連接
的中點(diǎn),連接![]() 交
交![]() 于
于![]() ,連接
,連接![]() ,過(guò)
,過(guò)![]() 作
作![]() 交
交![]() 的延長(zhǎng)線于
的延長(zhǎng)線于![]() ,則
,則![]() 的長(zhǎng)為________.
的長(zhǎng)為________.
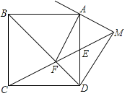
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,直線y=![]() x+4與x軸、y軸分別交于點(diǎn)A和點(diǎn)B,點(diǎn)C、D分別為線段AB、OB的中點(diǎn),點(diǎn)P為OA上一動(dòng)點(diǎn),當(dāng)PC+PD的值最小時(shí),點(diǎn)P的坐標(biāo)為( )
x+4與x軸、y軸分別交于點(diǎn)A和點(diǎn)B,點(diǎn)C、D分別為線段AB、OB的中點(diǎn),點(diǎn)P為OA上一動(dòng)點(diǎn),當(dāng)PC+PD的值最小時(shí),點(diǎn)P的坐標(biāo)為( )

A.(﹣1,0)B.(﹣2,0)C.(﹣3,0)D.(﹣4,0)
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專(zhuān)區(qū) | 電信詐騙舉報(bào)專(zhuān)區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專(zhuān)區(qū) | 涉企侵權(quán)舉報(bào)專(zhuān)區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com