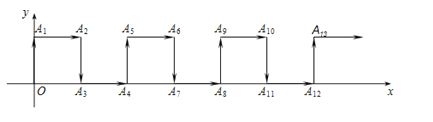
【題目】如圖，在平面直角坐標系中，一動點從原點
出發，按向上.向右.向下.向右的方向依次平移，每次移動一個單位，得到
（0，1），
（1，1），
（1，0），
（2，0），…那么點
的坐標為__________.
科目：初中數學 來源： 題型：
【題目】如圖，在△ABC中，按以下步驟作圖：
①以B為圓心，任意長為半徑作弧，交AB于D，交BC于E；
②分別以D，E為圓心，以大于
DE的同樣長為半徑作弧，兩弧交于點F；
③作射線BF交AC于G.
如果BG=CG，∠A=60°，那么∠ACB的度數為____________．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】某校七年級全體學生在5名教師的帶領下去公園秋游，公園的門票為每人30元.現有兩種優惠方案，甲方案：帶隊老師免費，學生按8折收費；乙方案：師生都按7.5折收費.
（1）若有n名學生，用含n的代數式表示兩種優惠方案各需多少元？
（2）當n=70時，采用哪種方案更優惠？
（3）當n=100時，采用哪種方案更優惠？
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】同學們都知道：|5﹣（﹣2）|表示5與﹣2之差的絕對值，實際上也可理解為5與﹣2兩數在數軸上所對應的兩點之間的距離．請你借助數軸進行以下探索：
（1）數軸上表示5與﹣2兩點之間的距離是 ，
（2）數軸上表示x與2的兩點之間的距離可以表示為 ．
（3）如果|x﹣2|=5，則x= ．
（4）同理|x+3|+|x﹣1|表示數軸上有理數x所對應的點到﹣3和1所對應的點的距離之和，請你找出所有符合條件的整數x，使得|x+3|+|x﹣1|=4，這樣的整數是 ．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】為了解黔東南州某縣2016屆中考學生的體育考試得分情況，從該縣參加體育考試的4 000名學生中隨機抽取了100名學生的體育考試成績作樣本分析，得出如下不完整的頻數統計表和頻數直方圖．
成績分組 | 頻數 |
25≤x<30 | 4 |
30≤x<35 | m |
35≤x<40 | 24 |
40≤x<45 | 36 |
45≤x<50 | n |
50≤x<55 | 4 |
(1)求m，n的值，并補全頻數直方圖；
(2)若體育得分在40分以上(包括40分)為優秀，請問該縣中考體育成績優秀的學生人數約為多少？
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】（請在括號里注明重要的推理依據）
如圖，已知AM∥BN，∠A=60°．點P是射線AM上一動點（與點A不重合），BC、BD分別平分∠ABP和∠PBN，分別交射線AM于點C，D．
（1）求∠CBD的度數；
（2）當點P運動時，∠APB與∠ADB之間的數量關系是否隨之發生變化？若不變化，請寫出它們之間的關系，并說明理由；若變化，請寫出變化規律．
（3）當點P運動到使∠ACB=∠ABD時，∠ABC的度數是 ．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在矩形OABC中，AO=10，AB=8，沿直線CD折疊矩形OABC的一邊BC，使點B落在OA邊上的點E處．分別以OC，OA所在的直線為x軸，y軸建立平面直角坐標系，拋物線y=ax2+bx+c經過O，D，C三點．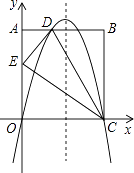
（1）求AD的長及拋物線的解析式；
（2）一動點P從點E出發，沿EC以每秒2個單位長的速度向點C運動，同時動點Q從點C出發，沿CO以每秒1個單位長的速度向點O運動，當點P運動到點C時，兩點同時停止運動．設運動時間為t秒，當t為何值時，以P、Q、C為頂點的三角形與△ADE相似？
（3）點N在拋物線對稱軸上，點M在拋物線上，是否存在這樣的點M與點N，使以M，N，C，E為頂點的四邊形是平行四邊形？若存在，請直接寫出點M與點N的坐標（不寫求解過程）；若不存在，請說明理由．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】已知在四邊形ABCD中，∠A=x，∠C=y，（0°＜x＜180°，0°＜y＜180°）．
（1）∠ABC+∠ADC=_____（用含x、y的代數式表示）；
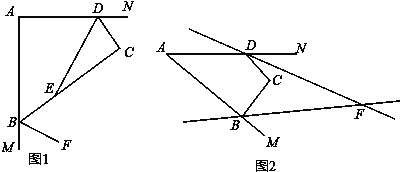
（2）如圖1，若x=y=90°，DE平分∠ADC，BF平分與∠ABC相鄰的外角，請寫出DE與BF的位置關系，并說明理由．
（3）如圖2，∠DFB為四邊形ABCD的∠ABC、∠ADC相鄰的外角平分線所在直線構成的銳角，
①當x＜y時，若x+y=140°，∠DFB=30°試求x、y．
②小明在作圖時，發現∠DFB不一定存在，請直接指出x、y滿足什么條件時，∠DFB不存在．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
