
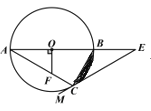
【題目】如圖,△ABC是⊙O的內接三角形,AB是⊙O的直徑,OF⊥AB,交AC于點F,點E在AB的延長線上,射線EM經過點C,且∠ACE+∠AFO=180°.
(1)求證:EM是⊙O的切線;
(2)若∠A=∠E,BC=![]() ,求陰影部分的面積.(結果保留
,求陰影部分的面積.(結果保留![]() 和根號).
和根號).
【答案】(1)詳見解析;(2)![]() ;
;
【解析】
(1)連接OC,根據垂直的定義得到∠AOF=90°,根據三角形的內角和得到∠ACE=90°+∠A,根據等腰三角形的性質得到∠OCE=90°,得到OC⊥CE,于是得到結論;
(2)根據圓周角定理得到∠ACB=90°,推出∠ACO=∠BCE,得到△BOC是等邊三角形,根據扇形和三角形的面積公式即可得到結論.
:(1)連接OC,
∵OF⊥AB,
∴∠AOF=90°,
∴∠A+∠AFO+90°=180°,
∵∠ACE+∠AFO=180°,
∴∠ACE=90°+∠A,
∵OA=OC,
∴∠A=∠ACO,
∴∠ACE=90°+∠ACO=∠ACO+∠OCE,
∴∠OCE=90°,
∴OC⊥CE,
∴EM是⊙O的切線;
(2)∵AB是⊙O的直徑,
∴∠ACB=90°,
∴∠ACO+∠BCO=∠BCE+∠BCO=90°,
∴∠ACO=∠BCE,
∵∠A=∠E,
∴∠A=∠ACO=∠BCE=∠E,
∴∠ABC=∠BCO+∠E=2∠A,
∴∠A=30°,
∴∠BOC=60°,
∴△BOC是等邊三角形,
∴OB=BC=![]() ,
,
∴陰影部分的面積=![]() ,
,


 舉一反三同步巧講精練系列答案
舉一反三同步巧講精練系列答案 口算與應用題卡系列答案
口算與應用題卡系列答案 名師點睛字詞句段篇系列答案
名師點睛字詞句段篇系列答案科目:初中數學 來源: 題型:
【題目】閱讀理解:法國數學家韋達在研究一元二次方程時有一項重大發現:如果一元二次方程![]() 的兩個根分別是
的兩個根分別是![]() ,那么
,那么![]() ,
,![]() .
.
例如:已知方程![]() 的兩根分別是
的兩根分別是![]() ,
,
則:![]() ,
,![]() .
.
請同學們閱讀后利用以上結論完成以下問題:
(1)已知方程![]() 的兩根分別是
的兩根分別是![]() ,求
,求![]() 和
和![]() 的值;
的值;
(2)已知方程![]() 的兩根分別是
的兩根分別是![]() ,且
,且![]() ,求
,求![]() 的值;
的值;
(3)若一元二次方程![]() 的一個根大于2,一個根小于2,求
的一個根大于2,一個根小于2,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】曉琳和爸爸到太子河公園運動,兩人同時從家出發,沿相同路線前行,途中爸爸有事返回,曉琳繼續前行5分鐘后也原路返回,兩人恰好同時到家.曉琳和爸爸在整個運動過程中離家的路程y1(米),y2(米)與運動時間x(分)之間的函數關系如圖所示,下列結論:①兩人同行過程中的速度為200米/分;②m的值是15,n的值是3000;③曉琳開始返回時與爸爸相距1800米;④運動18分鐘或30分鐘時,兩人相距900米.其中正確結論的個數是( )
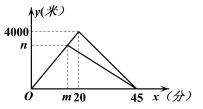
A. 1個 B. 2個 C. 3個 D. 4個
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】我省中小學積極開展綜合實踐活動,某校準備組織開展四項綜合實踐活動:“A.我是非遺小傳人,B.學做家常餐,C.愛心義賣行動,D.找個崗位去體驗”.為了解學生最喜愛哪項綜合實踐活動,隨機抽取部分學生進行問卷調查(每位學生只能選擇一項),將調查結果繪制成下面兩幅不完整的統計圖,請結合圖中提供的信息回答下列問題:
(1)本次一共調查了 名學生,在扇形統計圖中,m的值是 ;
(2)補全條形統計圖;
(3)若該校共有1200名學生,估計最喜愛B和C項目的學生一共有多少名?
(4)現有最喜愛A,B,C,D活動項目的學生各一人,學校要從這四人中隨機選取兩人交流活動體會,請用列表或畫樹狀圖的方法求出恰好選取最喜愛C和D項目的兩位學生的概率.
最喜愛各項綜合實踐活動條形統計圖 最喜愛各項綜合實踐活動扇形統計圖


查看答案和解析>>
科目:初中數學 來源: 題型:
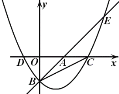
【題目】如圖,直線y=x-3與坐標軸交于A、B兩點,拋物線![]() 經過點B,與直線y=x-3交于點E(8,5),且與x軸交于C,D兩點.
經過點B,與直線y=x-3交于點E(8,5),且與x軸交于C,D兩點.
(1)求拋物線的解析式;
(2)拋物線上有一點M,當∠MBE=75°時,求點M的橫坐標;
(3)點P在拋物線上,在坐標平面內是否存在點Q,使得以點P,Q,B,C為頂點的四邊形是矩形?若存在,請直接寫出點Q的坐標;若不存在,請說明理由.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】小亮從家出發步行到公交站臺后,等公交車去學校,如圖, 折線表示這個過程中行程 s (千米)與所花時間 t (分)之間的關系,下 列說法錯誤的是( )
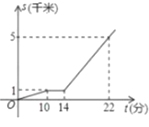
A.他家到公交車站臺需行 1 千米B.他等公交車的時間為 4 分鐘
C.公交車的速度是 500 米/分D.他步行與乘公交車行駛的平均速度300米/分鐘
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,兩個完全相同的三角形紙片![]() 和
和![]() 重合放置,其中
重合放置,其中![]() ,
,![]() .
.
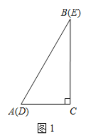

(1)操作發現:如圖2,固定![]() ,使
,使![]() 繞點
繞點![]() 旋轉,當點
旋轉,當點![]() 恰好落在
恰好落在![]() 邊上時,填空:①線段
邊上時,填空:①線段![]() 與
與![]() 的位置關系是________;②設
的位置關系是________;②設![]() 的面積為
的面積為![]() ,
,![]() 的面積為
的面積為![]() ,則
,則![]() 與
與![]() 的數量關系是_____.
的數量關系是_____.
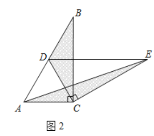
(2)猜想論證:當![]() 繞點
繞點![]() 旋轉到如圖3所示的位置時,請猜想(1)中
旋轉到如圖3所示的位置時,請猜想(1)中![]() 與
與![]() 的數量關系是否仍然成立?若成立,請證明;若不成立,請說明理由.
的數量關系是否仍然成立?若成立,請證明;若不成立,請說明理由.
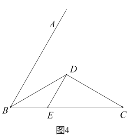
(3)拓展探究:已知![]() ,
,![]() 平分
平分![]() ,
,![]() ,
,![]() ,
,![]() 交
交![]() 于點
于點![]() (如圖4).若在射線
(如圖4).若在射線![]() 上存在點
上存在點![]() ,使
,使![]() ,請求相應的
,請求相應的![]() 的長.
的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某汽車租憑公司要購買轎車和面包車共![]() 輛,其中轎車最少要購買
輛,其中轎車最少要購買![]() 輛,轎車每輛
輛,轎車每輛![]() 萬元,購頭面包車每輛
萬元,購頭面包車每輛![]() 萬元,公司可投入的購車資金不超過
萬元,公司可投入的購車資金不超過![]() 萬元.
萬元.
(1)符合公司要求的購買方案有幾種?請說明理由;
(2)如果每輛轎車日租金為![]() 元,每輛面包車日租金為
元,每輛面包車日租金為![]() 元,假設新購買的這
元,假設新購買的這![]() 輛汽車每日都可以全部租出,公司希望
輛汽車每日都可以全部租出,公司希望![]() 輛汽車的日租金最高,那么應該選擇以上的哪種購買方案?且日租金最高為多少元?
輛汽車的日租金最高,那么應該選擇以上的哪種購買方案?且日租金最高為多少元?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com