
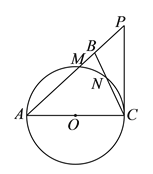
【題目】如圖,在![]() 中,
中,![]() ,以
,以![]() 為直徑的⊙
為直徑的⊙![]() 分別交
分別交![]() 、
、![]() 于點
于點![]() 、
、![]() ,點
,點![]() 在
在![]() 的延長線上,且
的延長線上,且![]() .
.
(![]() )求證:直線
)求證:直線![]() 是⊙
是⊙![]() 的切線.
的切線.
(![]() )若
)若![]() ,
,![]() ,求點
,求點![]() 到
到![]() 的距離.
的距離.
(![]() )在第(
)在第(![]() )的條件下,求
)的條件下,求![]() 的周長.
的周長.
【答案】(1)證明見解析;(2)點![]() 到
到![]() 的距離為
的距離為![]() ;(3)
;(3)![]() 的周長為
的周長為![]() .
.
【解析】試題分析:(1)根據∠ABC=∠ACB且∠CAB=2∠BCP,在△ABC中∠ABC+∠BAC+∠BCA=180°,得到2∠BCP+2∠BCA=180°,從而得到∠BCP+∠BCA=90°,證得直線CP是 O的切線.(2)作BD⊥AC于點D,得到BD∥PC,從而利用sin∠BCP=sin∠DBC=![]() ,求得DC=2,再根據勾股定理求得點B到AC的距離為4.(3)先求出AC的長度,然后利用BD∥PC的比例線段關系求得CP的長度,再由勾股定理求出AP的長度,從而求得△ACP的周長.
,求得DC=2,再根據勾股定理求得點B到AC的距離為4.(3)先求出AC的長度,然后利用BD∥PC的比例線段關系求得CP的長度,再由勾股定理求出AP的長度,從而求得△ACP的周長.
試題解析:(![]() )∵
)∵![]() 且
且![]() ,
,
在![]() 中,
中,![]() ,
,
∴![]() ,
,
∴![]() ,
,
又∵點![]() 在直徑上,
在直徑上,
∴直線![]() 是
是![]() 的切線.
的切線.
(![]() )如圖,作
)如圖,作![]() 于
于![]() ,
,
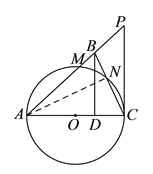
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴由勾股定理得![]() ,
,
∴點![]() 到
到![]() 的距離為
的距離為![]() .
.
(![]() )連接
)連接![]() ,∵
,∵![]() 為直徑,
為直徑,
∴![]() ,
,
∴![]() 中,
中,
![]() ,
,
又∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,∴
,∴![]()
在![]() 中,
中,![]() ,
,
![]() ,
,
∴![]() 的周長為
的周長為![]() .
.


科目:初中數學 來源: 題型:
【題目】如圖,直線AB:y=一 ![]() x+2與x軸相交于點A,與y軸交于點B.直線CD:y=kx+b經過點c(一1,0),D(0,
x+2與x軸相交于點A,與y軸交于點B.直線CD:y=kx+b經過點c(一1,0),D(0, ![]() ),與直線AB交于點E.
),與直線AB交于點E.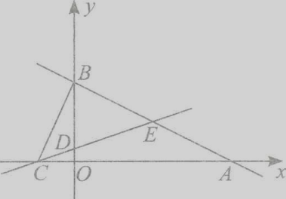
(1)求直線CD的函數關系式;
(2)連接BC,求△BCE的面積;
(3)設點Q的坐標為(m,2),求m的值使得QA+QE值最小.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖是根據寶塔山公園的平面示意圖建立的平面直角坐標系,公園的入口位于坐標原點O,古塔位于點A(﹣400,300),從古塔出發沿射線OA方向前行300m是盆景園B,從盆景園B向右轉90°后直行400m到達櫻花園C,則點C的坐標是 . 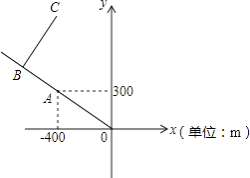
查看答案和解析>>
科目:初中數學 來源: 題型:
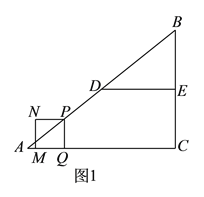
【題目】如圖![]() ,在
,在![]() 中,
中,![]() ,
,![]() ,
,![]() 、
、![]() 分別為邊
分別為邊![]() 、
、![]() 的中點,連結
的中點,連結![]() ,點
,點![]() 從點
從點![]() 出發,沿折線
出發,沿折線![]() 運動,到點
運動,到點![]() 停止,點
停止,點![]() 在
在![]() 上以
上以![]() 的速度運動,在
的速度運動,在![]() 上以
上以![]() 的速度運動,過點
的速度運動,過點![]() 作
作![]() 于點
于點![]() ,以
,以![]() 為邊作正方形
為邊作正方形![]() .設點
.設點![]() 的運動時間為
的運動時間為![]() .
.
(![]() )當點
)當點![]() 在線段
在線段![]() 上運動時,線段
上運動時,線段![]() 的長為__________
的長為__________![]() .(用含
.(用含![]() 的代數式表示)
的代數式表示)
(![]() )當正方形
)當正方形![]() 與
與![]() 重疊部分圖形為五邊形時,設五邊形的面積為
重疊部分圖形為五邊形時,設五邊形的面積為![]() ,求
,求![]() 與
與![]() 的函數關系式,并寫出
的函數關系式,并寫出![]() 的取值范圍.
的取值范圍.
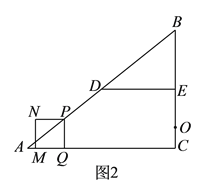
(![]() )如圖
)如圖![]() ,若點
,若點![]() 在線段
在線段![]() 上,且
上,且![]() ,以點
,以點![]() 為圓心,
為圓心,![]() 長為半徑作圓,當點
長為半徑作圓,當點![]() 開始運動時,⊙
開始運動時,⊙![]() 的半徑以
的半徑以![]() 的速度開始不斷增大,當⊙
的速度開始不斷增大,當⊙![]() 與正方形
與正方形![]() 的邊所在直線相切時,求此時的
的邊所在直線相切時,求此時的![]() 值.
值.
查看答案和解析>>
科目:初中數學 來源: 題型:
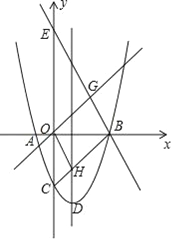
【題目】如圖,拋物線y=x2﹣(m+2)x+3(m﹣1)與x軸的兩個交點為A、B,與y軸交于點C,點D為拋物線的頂點,直線y=﹣2x+m+6經過點B,交y軸于點E(0,6).
(1)求直線和拋物線的解析式;
(2)如果拋物線的對稱軸與線段BC交于點H,且直線y=x與直線y=﹣2x+m+6交于點G,求證:四邊形OHBG是平行四邊形;
(3)在拋物線上是否存在點P,使△APB的面積等于平行四邊形OHBG的面積,若存在,直接寫出P點的坐標,若不存在請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知:△ABC≌△DCB,若BC=10cm,AB=6cm,AC=7cm,則CD為( )
A. 10cm B. 7cm C. 6cm D. 6cm或7cm
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】初步測算,2015年海寧市全年實現地區生產總值700.23億元,比上年增長6.7%.其中700.23億用科學記數法表示為( )
A.700.23×108
B.70.023×109
C.7.0023×1010
D.7.0023×109
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com