
【題目】如圖,在△ABC中,AB=AC,E在CA延長線上,AE=AF,AD是高,試判斷EF與BC的位置關系,并說明理由. 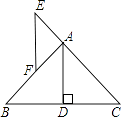
【答案】解:EF⊥BC,理由為: 證明:∵AB=AC,AD⊥BC,
∴∠BAD=∠CAD,
∵AE=AF,
∴∠E=∠EFA,
∵∠BAC=∠E+∠EFA=2∠EFA,
∴∠EFA=∠BAD,
∴EF∥AD,
∵AD⊥BC,
∴EF⊥BC,
則EF與BC的位置關系是垂直.
【解析】EF與BC垂直,理由為:由三角形ABC為等腰三角形且AD為底邊上的高,利用三線合一得到AD為角平分線,再由AE=AF,利用等邊對等角得到一對角相等,利用外角性質得到一對內錯角相等,利用內錯角相等兩直線平行得到EF與AD平行,進而確定出EF與BC垂直.
【考點精析】根據題目的已知條件,利用等腰三角形的性質的相關知識可以得到問題的答案,需要掌握等腰三角形的兩個底角相等(簡稱:等邊對等角).


科目:初中數學 來源: 題型:
【題目】如圖,直線l1∥l2∥l3 , 且l1與l2的距離為1,l2與l3的距離為3.把一塊含有45°角的直角三角板如圖放置,頂點A、B、C恰好分別落在三條直線上,則△ABC的面積為 . 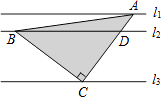
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】有一道題,已知線段AB=a,在直線AB上取一點C,使BC=b(a>b),點M,N分別是線段AB,BC的中點,求線段MN的長.對這道題,小善同學的答案是7,小昌同學的答案是3.老師說他們的結果都沒錯,如圖,則依次可得到a的值是 . ![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】若A、B兩點在數軸上所表示的數分別為a、b,則A、B兩點間的距離可記為|a﹣b|:
(1)如圖:若A、B兩點在數軸上所表示的數分別為﹣2、4,求A、B兩點的距離為;![]()
(2)若A,B兩點分別以每秒3個單位長度和每秒1個單位長度的速度同時沿數軸正方向運動,設運動時間為t秒,解答下列問題:
①運動t秒后,A點所表示的數為 , B點所表示的數為;(答案均用含t的代數式表示)
②當t為何值時,A、B兩點的距離為4?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】閱讀下列材料:
根據聯合國《人口老齡化及其社會經濟后果》中提到的標準,當一個國家或地區65歲及以上老年人口數量占總人口比例超過7%時,意味著這個國家或地區進入老齡化。從經濟角度,一般可用“老年人口撫養比”來反映人口老齡化社會的后果。所謂“老年人口撫養比”是指某范圍人口中,老年人口數(65歲及以上人口數)與勞動年齡人口數(15-64歲人口數)之比,通常用百分比表示,用以表明每100名勞動年齡人口要負擔多少名老年人。
以下是根據我國近幾年的人口相關數據制作的統計圖和統計表。
2011-2014年全國人口年齡分布圖

2011-2014年全國人口年齡分布表
2011年 | 2012年 | 2013年 | 2014年 | |
0-14歲人口占總人口的百分比 | 16.4% | 16.5% | 16.4% | 16.5% |
15-64歲人口占總人口的百分比 | 74.5% | 74.1% | 73.9% | 73.5% |
65歲及以上人口占總人口的百分比 | m | 9.4% | 9.7% | 10.0% |
*以上圖表中數據均為年末的數據。
根據以上材料解答下列問題:
(1)2011年末,我國總人口約為_______億,全國人口年齡分布表中m的值為_______;
(2)若按目前我國的人口自然增長率推測,到2027年末我國約有14.60億人。假設0-14歲人口占總人口的百分比一直穩定在16.5%,15-64歲的人口一直穩定在10億,那么2027年末我國0-14歲人口約為_______億,“老年人口撫養比”約為_______; (精確到1%)
(3)2016年1月1日起我國開始施行“全面二孩”政策,一對夫妻可生育兩個孩子。在未來10年內,假設出生率顯著提高,這_______(填“會”或“不會”)對我國的“老年人口撫養比”產生影響。
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com