
【題目】如圖,在![]() 中,AB=AC,AD平分∠BAC交BC于點(diǎn)D,在線段AD上任取一點(diǎn)P(點(diǎn)A除外),過點(diǎn)P作EF∥AB.分別交AC、BC于點(diǎn)E和點(diǎn)F,作PQ∥AC,交AB于點(diǎn)Q,連接QE.
中,AB=AC,AD平分∠BAC交BC于點(diǎn)D,在線段AD上任取一點(diǎn)P(點(diǎn)A除外),過點(diǎn)P作EF∥AB.分別交AC、BC于點(diǎn)E和點(diǎn)F,作PQ∥AC,交AB于點(diǎn)Q,連接QE.
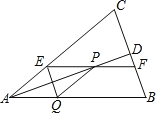
(1)求證:四邊形AEPQ為菱形:
(2)當(dāng)點(diǎn)P在線段EF上的什么位置時(shí),菱形AEPQ的面積為四邊形EFBQ面積的一半?請(qǐng)說明理
【答案】(1)見解析;(2)P為EF中點(diǎn)時(shí),S菱形AEPQ=12S四邊形EFBQ,理由見解析.
【解析】
(1)先證出四邊形AEPQ為平行四邊形,關(guān)鍵是找一組鄰邊相等,由AD平分∠BAC和PE∥AQ可證∠EAP=∠EPA,得出AE=EP,即可得出結(jié)論;
(2)S菱形AEPQ=EPh,S平行四邊形EFBQ=EFh,若菱形AEPQ的面積為四邊形EFBQ面積的一半,則EP=![]() EF,因此P為EF中點(diǎn)時(shí),S菱形AEPQ=
EF,因此P為EF中點(diǎn)時(shí),S菱形AEPQ=![]() S四邊形EFBQ.
S四邊形EFBQ.
(1)證明:∵EF∥AB,PQ∥AC,
∴四邊形AEPQ為平行四邊形.
∵AB=AC,AD平分∠CAB,
∴∠CAD=∠BAD,
∵∠BAD=∠EPA,
∴∠CAD=∠EPA,
∴EA=EP,
∴四邊形AEPQ為菱形.
(2)P為EF中點(diǎn)時(shí),S菱形AEPQ=![]() S四邊形EFBQ
S四邊形EFBQ
∵四邊形AEPQ為菱形,
∴AD⊥EQ,
∵AD⊥BC,
∴EQ∥BC,
又∵EF∥AB,
∴四邊形EFBQ為平行四邊形.
作EN⊥AB于N,如圖所示:

則S菱形AEPQ=EPEN=![]() EFEN=
EFEN=![]() S四邊形EFBQ
S四邊形EFBQ



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:
【題目】為了提高學(xué)生書寫漢字的能力,增強(qiáng)保護(hù)漢子的意識(shí),某校舉辦了首屆“漢字聽寫大賽”,學(xué)生經(jīng)選拔后進(jìn)入決賽,測(cè)試同時(shí)聽寫100個(gè)漢字,每正確聽寫出一個(gè)漢字得1分,本次決賽,學(xué)生成績(jī)?yōu)?/span>![]() (分),且
(分),且![]() ,將其按分?jǐn)?shù)段分為五組,繪制出以下不完整表格:
,將其按分?jǐn)?shù)段分為五組,繪制出以下不完整表格:
組別 | 成績(jī) | 頻數(shù)(人數(shù)) | 頻率 |
一 |
| 2 | 0.04 |
二 |
| 10 | 0.2 |
三 |
| 14 | b |
四 |
| a | 0.32 |
五 |
| 8 | 0.16 |
請(qǐng)根據(jù)表格提供的信息,解答以下問題:
(1)本次決賽共有 名學(xué)生參加;
(2)直接寫出表中a= ,b= ;
(3)請(qǐng)補(bǔ)全下面相應(yīng)的頻數(shù)分布直方圖;

(4)若決賽成績(jī)不低于80分為優(yōu)秀,則本次大賽的優(yōu)秀率為 。
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖所示,已知![]() 中,
中,![]() 厘米,
厘米,![]() 、
、![]() 分別從點(diǎn)
分別從點(diǎn)![]() 、點(diǎn)
、點(diǎn)![]() 同時(shí)出發(fā),沿三角形的邊運(yùn)動(dòng),已知點(diǎn)
同時(shí)出發(fā),沿三角形的邊運(yùn)動(dòng),已知點(diǎn)![]() 的速度是1厘米/秒的速度,點(diǎn)
的速度是1厘米/秒的速度,點(diǎn)![]() 的速度是2厘米/秒,當(dāng)點(diǎn)
的速度是2厘米/秒,當(dāng)點(diǎn)![]() 第一次到達(dá)
第一次到達(dá)![]() 點(diǎn)時(shí),
點(diǎn)時(shí),![]() 、
、![]() 同時(shí)停止運(yùn)動(dòng).
同時(shí)停止運(yùn)動(dòng).
(1)![]() 、
、![]() 同時(shí)運(yùn)動(dòng)幾秒后,
同時(shí)運(yùn)動(dòng)幾秒后,![]() 、
、![]() 兩點(diǎn)重合?
兩點(diǎn)重合?
(2)![]() 、
、![]() 同時(shí)運(yùn)動(dòng)幾秒后,可得等邊三角形
同時(shí)運(yùn)動(dòng)幾秒后,可得等邊三角形![]() ?
?
(3)![]() 、
、![]() 在
在![]() 邊上運(yùn)動(dòng)時(shí),能否得到以
邊上運(yùn)動(dòng)時(shí),能否得到以![]() 為底邊的等腰
為底邊的等腰![]() ,如果存在,請(qǐng)求出此時(shí)
,如果存在,請(qǐng)求出此時(shí)![]() 、
、![]() 運(yùn)動(dòng)的時(shí)間?
運(yùn)動(dòng)的時(shí)間?

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,四邊形ABCD為平行四邊形,延長AD到E,使DE=AD,連接EB,EC,DB.添加一個(gè)條件,不能使四邊形DBCE成為矩形的是( )

(A)AB=BE (B)BE⊥DC (C)∠ADB=90° (D)CE⊥DE
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,在![]() 中,
中,![]() 平分
平分![]() ,交
,交![]() 于點(diǎn)E,
于點(diǎn)E,![]() 平分
平分![]() ,交
,交![]() 于點(diǎn)F,
于點(diǎn)F,![]() 與
與![]() 交于點(diǎn)P,連結(jié)
交于點(diǎn)P,連結(jié)![]() ,
,![]() .
.

(1)求證:四邊形![]() 是菱形.
是菱形.
(2)若![]() ,
,![]() ,
,![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,點(diǎn)P是矩形ABCD的邊上一動(dòng)點(diǎn),矩形兩邊長AB、BC長分別為15和20,那么P到矩形兩條對(duì)角線AC和BD的距離之和是( )
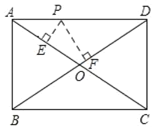
A.6B.12C.24D.不能確定
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】已知關(guān)于![]() 的一元二次方程
的一元二次方程![]() 有兩個(gè)實(shí)數(shù)根.
有兩個(gè)實(shí)數(shù)根.
![]() 若
若![]() 為正整數(shù),求此方程的根.
為正整數(shù),求此方程的根.
![]() 設(shè)此方程的兩個(gè)實(shí)數(shù)根為
設(shè)此方程的兩個(gè)實(shí)數(shù)根為![]() 、
、![]() ,若
,若![]() ,求
,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,一次函數(shù)的圖象過![]() 兩點(diǎn).
兩點(diǎn).

(1)求直線![]() 的函數(shù)表達(dá)式
的函數(shù)表達(dá)式
(2)直線![]() 交
交![]() 軸于點(diǎn)
軸于點(diǎn)![]() 為直線
為直線![]() 上一動(dòng)點(diǎn)
上一動(dòng)點(diǎn)
①求![]() 的最小值;
的最小值;
②![]() 是直線
是直線![]() 上任意一點(diǎn),
上任意一點(diǎn),![]() 為直線
為直線![]() 上另一動(dòng)點(diǎn),若
上另一動(dòng)點(diǎn),若![]() 是以
是以![]() 為直角邊長的等腰直角三角形,求
為直角邊長的等腰直角三角形,求![]() 點(diǎn)的坐標(biāo).
點(diǎn)的坐標(biāo).
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖是二次函數(shù)y=ax2+bx+c(a≠0)圖象的一部分,對(duì)稱軸為x=![]() ,且經(jīng)過點(diǎn)(2,0),有下列說法:①abc<0;②a+b=0;③4a+2b+c<0;④若(0,y1),(1,y2)是拋物線上的兩點(diǎn),則y1=y2.上述說法正確的是( )
,且經(jīng)過點(diǎn)(2,0),有下列說法:①abc<0;②a+b=0;③4a+2b+c<0;④若(0,y1),(1,y2)是拋物線上的兩點(diǎn),則y1=y2.上述說法正確的是( )

A.①②④ B.③④ C.①③④ D.①②
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com