Question

【題目】已知定點 ， 為圓 上任意一點，線段 上一點 滿足 ，直線 上一點 ，滿足 .
（1）當 在圓周上運動時，求點 的軌跡 的方程；
（2）若直線 與曲線 交于 兩點，且以 為直徑的圓過原點 ，求證：直線 與 不可能相切.

Answer 1

【答案】
（1）解：由 ，直線 上一點 ，滿足 ，可得 時線段 的垂直平分線，求出圓 的圓心坐標為 ，半徑為 ，得到 ，點Q的軌跡是以F1、F2為焦點，長軸長為 的橢圓，即2a= ，2c= ，∴b= ．
所以點Q的軌跡C的方程為：
（2）解：當直線的斜率存在時，設直線l為y=kx+m ， A（x1 ， y1），B（x2 ， y2），聯立直線與橢圓的方程，
得 消去y并整理得（1+2k2）x2+4kmx+2m2-6=0．
因為直線與橢圓有兩個不同的交點，所以
△=16k2m2-4（1+2k2）（2m2-6）＞0，化簡得：m2＜6k2+3①
由韋達定理得： ．
∴ ．
∵ ，∴x1x2+y1y2=0，即 ，
整理得m2=2k2+2滿足①式，∴d= ，即原點到直線l為的距離是 ，
∴直線l與圓x2+y2=4相交．
當直線的斜率不存在時，直線為x=m ， 與橢圓C交點為A（m ， ），B（m ， ）
∵ ，∴ ．
此時直線為x= ，顯然也與圓x2+y2=4相交．
綜上，直線l與定圓E：x2+y2=4不可能相切
【解析】（1）本題最重數形結合的思想，先畫出草圖，將數據標到圖上，使題目清晰化。再根據線段長度之間的關系，得到Q點到F1 ， F2兩點的距離之和為一定值，且大于F1和F2間的距離，故滿足橢圓定義，可知曲線C是一橢圓，即可得到結果。
（2）先根據條件設出直線，聯立消元得到一元二次方程，由相交于兩點可得；以AB為直徑的圓過原點，故可得；，由以上兩個條件可得k和m關系，然后用點到直線的距離公式，看原點到直線的距離是否滿足證明，即距離不等于2。
【考點精析】利用點到直線的距離公式和橢圓的概念對題目進行判斷即可得到答案，需要熟知點到直線的距離為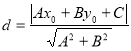：；平面內與兩個定點，的距離之和等于常數（大于）的點的軌跡稱為橢圓,這兩個定點稱為橢圓的焦點，兩焦點的距離稱為橢圓的焦距．