
【題目】在數(shù)列{an}中,a1=1,an+1=(1+ ![]() )an+
)an+ ![]() .
.
(1)設(shè)bn= ![]() ,求數(shù)列{bn}的通項(xiàng)公式;
,求數(shù)列{bn}的通項(xiàng)公式;
(2)求數(shù)列{an}的前n項(xiàng)和Sn .
【答案】
(1)解:由已知得b1=a1=1,且 ![]() =
= ![]() +
+ ![]() ,
,
即bn+1=bn+ ![]() ,從而b2=b1+
,從而b2=b1+ ![]() ,
,
b3=b2+ ![]() ,
,
bn=bn﹣1+ ![]() (n≥2).
(n≥2).
于是bn=b1+ ![]() +
+ ![]() +…+
+…+ ![]() =2﹣
=2﹣ ![]() (n≥2).
(n≥2).
又b1=1,
故所求的通項(xiàng)公式為bn=2﹣ ![]()
(2)解:由(1)知an=2n﹣ ![]() ,
,
故Sn=(2+4+…+2n)﹣(1+ ![]() +
+ ![]() +
+ ![]() +…+
+…+ ![]() ),
),
設(shè)Tn=1+ ![]() +
+ ![]() +
+ ![]() +…+
+…+ ![]() ,①
,①
![]() Tn=
Tn= ![]() +
+ ![]() +
+ ![]() +…+
+…+ ![]() +
+ ![]() ,②
,②
①﹣②得,
![]() Tn=1+
Tn=1+ ![]() +
+ ![]() +
+ ![]() +…+
+…+ ![]() ﹣
﹣ ![]()
= ![]() ﹣
﹣ ![]() =2﹣
=2﹣ ![]() ﹣
﹣ ![]() ,
,
∴Tn=4﹣ ![]() .
.
∴Sn=n(n+1)+ ![]() ﹣4
﹣4
【解析】(1)由已知得 ![]() =
= ![]() +
+ ![]() ,即bn+1=bn+
,即bn+1=bn+ ![]() ,由此能夠推導(dǎo)出所求的通項(xiàng)公式.(2)由題設(shè)知an=2n﹣
,由此能夠推導(dǎo)出所求的通項(xiàng)公式.(2)由題設(shè)知an=2n﹣ ![]() ,故Sn=(2+4+…+2n)﹣(1+
,故Sn=(2+4+…+2n)﹣(1+ ![]() +
+ ![]() +
+ ![]() +…+
+…+ ![]() ),設(shè)Tn=1+
),設(shè)Tn=1+ ![]() + +
+ + ![]() +…+
+…+ ![]() ,由錯(cuò)位相減法能求出Tn=4﹣
,由錯(cuò)位相減法能求出Tn=4﹣ ![]() .從而導(dǎo)出數(shù)列{an}的前n項(xiàng)和Sn .
.從而導(dǎo)出數(shù)列{an}的前n項(xiàng)和Sn .
【考點(diǎn)精析】利用數(shù)列的前n項(xiàng)和和數(shù)列的通項(xiàng)公式對(duì)題目進(jìn)行判斷即可得到答案,需要熟知數(shù)列{an}的前n項(xiàng)和sn與通項(xiàng)an的關(guān)系 ;如果數(shù)列an的第n項(xiàng)與n之間的關(guān)系可以用一個(gè)公式表示,那么這個(gè)公式就叫這個(gè)數(shù)列的通項(xiàng)公式.
;如果數(shù)列an的第n項(xiàng)與n之間的關(guān)系可以用一個(gè)公式表示,那么這個(gè)公式就叫這個(gè)數(shù)列的通項(xiàng)公式.



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
【題目】(本小題滿分為16分)已知函數(shù)![]() .
.
(1)若![]() ,求函數(shù)
,求函數(shù)![]() 的極值,并指出極大值還是極小值;
的極值,并指出極大值還是極小值;
(2)若![]() ,求函數(shù)
,求函數(shù)![]() 在
在![]() 上的最值;
上的最值;
(3)若![]() ,求證:在區(qū)間
,求證:在區(qū)間![]() 上,函數(shù)
上,函數(shù)![]() 的圖象在
的圖象在![]() 的圖象下方.
的圖象下方.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知命題p:x∈[1,2],x2﹣a≥0,命題q:x0∈R,使得x02+(a﹣1)x0﹣1<0,若p∨q為真,p∧q為假,求實(shí)數(shù)a的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】下面有五個(gè)命題:
①函數(shù)y=sin4θ﹣cos4θ的最小正周期是π;
②終邊在y軸上的角的集合是 ![]() ;
;
③把 ![]() 的圖象向右平移
的圖象向右平移 ![]() 得到y(tǒng)=3sin2x的圖象;
得到y(tǒng)=3sin2x的圖象;
④函數(shù) ![]() 在[0,π]是減函數(shù);
在[0,π]是減函數(shù);
其中真命題的序號(hào)是(寫出所有真命題的序號(hào))
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】(本題滿分16分)已知函數(shù)![]() ,
, ![]() .
.
(1)若函數(shù)![]() 在
在![]() 上單調(diào)遞增,求實(shí)數(shù)
上單調(diào)遞增,求實(shí)數(shù)![]() 的取值范圍;
的取值范圍;
(2)若直線![]() 是函數(shù)
是函數(shù)![]() 圖象的切線,求
圖象的切線,求![]() 的最小值;
的最小值;
(3)當(dāng)![]() 時(shí),若
時(shí),若![]() 與
與![]() 的圖象有兩個(gè)交點(diǎn)
的圖象有兩個(gè)交點(diǎn)![]() ,求證:
,求證: ![]()
![]() .(取
.(取![]() 為
為![]() ,取
,取![]() 為
為![]() ,取
,取![]() 為
為![]() )
)
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,在三棱錐P﹣ABC中,PA⊥底面ABC,∠ACB=90°,AE⊥PB于E,AF⊥PC于F,若PA=AB=2,∠BPC=θ,則當(dāng)△AEF的面積最大時(shí),tanθ的值為( ) 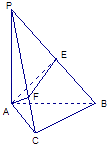
A.2
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)f(x)=ax3+bx+c在點(diǎn)x=2處取得極值c﹣16. (Ⅰ)求a,b的值;
(Ⅱ)若f(x)有極大值28,求f(x)在[﹣3,3]上的最小值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】設(shè)對(duì)于任意實(shí)數(shù)x,不等式|x+7|+|x﹣1|≥m恒成立.
(1)求m的取值范圍;
(2)當(dāng)m取最大值時(shí),解關(guān)于x的不等式:|x﹣3|﹣2x≤2m﹣12.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】
如圖,⊙O內(nèi)切于△ABC的邊于D,E,F(xiàn),AB=AC,連接AD交⊙O于點(diǎn)H,直線HF交BC的延長(zhǎng)線于點(diǎn)G.
(Ⅰ)求證:圓心O在直線AD上;
(Ⅱ)求證:點(diǎn)C是線段GD的中點(diǎn).

查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com