Question

【題目】將邊長為a的正方形ABCD沿對角線AC折起，使得BD=a.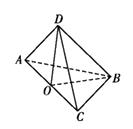

（1）求證：平面 平面ABC；
（2）求三棱錐D-ABC的體積.

Answer 1

【答案】
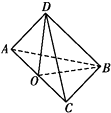
（1）解：如圖，取AC的中點 ，連 ．

則 ，
又 ，
所以 ,
所以 ．
又 ,
所以 平面 ,
因為 平面 ，
所以平面 平面
（2）解：由（1）知 平面 ，
所以 ，
即三棱錐 的體積為
【解析】（1）根據正方形的性質得到AC分別與OB、OD垂直，得到平面ADC與平面ABC所成二面角的平面角，利用勾股定理證明該角為直角，從而證明兩平面垂直。
（2）根據（1）的結論，證明OD是三棱錐的高，根據三棱錐的體積公式求解。
【考點精析】通過靈活運用平面與平面垂直的判定和平面與平面垂直的性質，掌握一個平面過另一個平面的垂線，則這兩個平面垂直；兩個平面垂直，則一個平面內垂直于交線的直線與另一個平面垂直即可以解答此題．