
【題目】已知函數f(x)是定義在區間[﹣1,1]上的奇函數,且f(1)=1,若對于任意的m、n∈[﹣1,1]有 ![]() .
.
(1)判斷并證明函數的單調性;
(2)解不等式 ![]() ;
;
(3)若f(x)≤﹣2at+2對于任意的x∈[﹣1,1],a∈[﹣1,1]恒成立,求實數t的取值范圍.
【答案】
(1)函數f(x)在區間[﹣1,1]上是增函數:
證明:由題意可知,對于任意的m、n∈[﹣1,1]有 ![]() ,
,
可設x1=m,x2=﹣n,則 ![]() ,即
,即 ![]() ,
,
當x1>x2時,f(x1)>f(x2),
∴函數f(x)在區間[﹣1,1]上是增函數;
當x1<x2時,f(x1)<f(x2),
∴函數f(x)在區間[﹣1,1]上是增函數;
綜上:函數f(x)在區間[﹣1,1]上是增函數
(2)由(1)知函數f(x)在區間[﹣1,1]上是增函數,
又由 ![]() ,
,
得 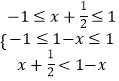 ,解得
,解得 ![]() ,
,
∴不等式 ![]() 的解集為
的解集為 ![]()
(3)∵函數f(x)在區間[﹣1,1]上是增函數,且f(1)=1,
要使得對于任意的x∈[﹣1,1],a∈[﹣1,1]都有f(x)≤﹣2at+2恒成立,
只需對任意的a∈[﹣1,1]時﹣2at+2≥1,即﹣2at+1≥0恒成立,
令y=﹣2at+1,此時y可以看做a的一次函數,且在a∈[﹣1,1]時y≥0恒成立,
因此只需要 ![]() ,解得
,解得 ![]() ,
,
∴實數t的取值范圍為: ![]()
【解析】(1)設x1=m,x2=﹣n,由已知可得 ![]() ,分x1>x2 , 及x1<x2兩種情況可知f(x1)與f(x2)的大小,借助單調性的定義可得結論;(2)利用函數單調性可得去掉不等式中的符號“f”,轉化為具體不等式,再考慮到函數定義域可得不等式組,解出即可;(3)要使得對于任意的x∈[﹣1,1],a∈[﹣1,1]都有f(x)≤﹣2at+2恒成立,只需對任意的a∈[﹣1,1]時﹣2at+2≥f(x)max , 整理后化為關于a的一次函數可得不等式組;
,分x1>x2 , 及x1<x2兩種情況可知f(x1)與f(x2)的大小,借助單調性的定義可得結論;(2)利用函數單調性可得去掉不等式中的符號“f”,轉化為具體不等式,再考慮到函數定義域可得不等式組,解出即可;(3)要使得對于任意的x∈[﹣1,1],a∈[﹣1,1]都有f(x)≤﹣2at+2恒成立,只需對任意的a∈[﹣1,1]時﹣2at+2≥f(x)max , 整理后化為關于a的一次函數可得不等式組;
【考點精析】解答此題的關鍵在于理解奇偶性與單調性的綜合的相關知識,掌握奇函數在關于原點對稱的區間上有相同的單調性;偶函數在關于原點對稱的區間上有相反的單調性.


 提分百分百檢測卷單元期末測試卷系列答案
提分百分百檢測卷單元期末測試卷系列答案 小學期末標準試卷系列答案
小學期末標準試卷系列答案科目:高中數學 來源: 題型:
【題目】如圖,在三棱錐P﹣ABC中,PA⊥平面ABC,AC⊥BC,D為側棱PC的中點,它的正(主)視圖和側(左)視圖如圖所示. 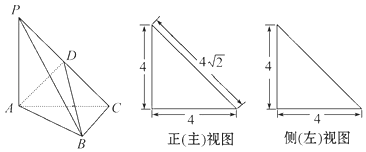
(Ⅰ)求三棱錐P﹣ABD的體積.
(Ⅱ)在∠ACB的平分線所在直線上確定一點Q,使得PQ∥平面ABD,并求此時PQ的長.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() ,圓
,圓![]() 的圓心
的圓心![]() 在橢圓
在橢圓![]() 上,點
上,點![]() 到橢圓
到橢圓![]() 的右焦點的距離為
的右焦點的距離為![]() .
.

(1)求橢圓![]() 的方程;
的方程;
(2)過點![]() 作互相垂直的兩條直線
作互相垂直的兩條直線![]() ,且
,且![]() 交橢圓
交橢圓![]() 于
于![]() 兩點, 直線
兩點, 直線![]() 交圓
交圓![]() 于
于![]() 兩點, 且
兩點, 且![]() 為
為![]() 的中點, 求
的中點, 求![]() 的面積的取值范圍.
的面積的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)= ![]() +
+ ![]() 的兩個極值點分別為x1 , x2 , 且x1∈(0,1),x2∈(1,+∞);點P(m,n)表示的平面區域為D,若函數y=loga(x+4)(a>1)的圖象上存在區域D內的點,則實數a的取值范圍是( )
的兩個極值點分別為x1 , x2 , 且x1∈(0,1),x2∈(1,+∞);點P(m,n)表示的平面區域為D,若函數y=loga(x+4)(a>1)的圖象上存在區域D內的點,則實數a的取值范圍是( )
A.(1,3]
B.(1,3)
C.(3,+∞)
D.[3,+∞)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】海水養殖場進行某水產品的新、舊網箱養殖方法的產量對比,收獲時各隨機抽取了100個網箱,測量各箱水產品的產量(單位:kg)其頻率分布直方圖如下:
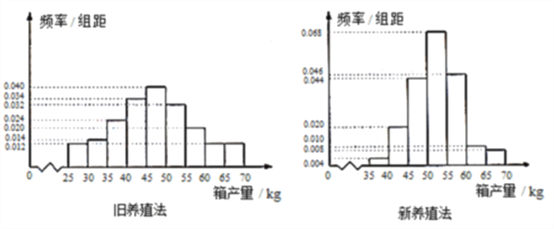
(1) 記![]() 表示事件“舊養殖法的箱產量低于50kg”,估計
表示事件“舊養殖法的箱產量低于50kg”,估計![]() 的概率;
的概率;
(2)填寫下面聯表,并根據列聯表判斷是否有![]() %的把握認為箱產量與養殖方法有關:
%的把握認為箱產量與養殖方法有關:
箱產量 | 箱產量 | |
舊養殖法 | ||
新養殖法 |
(3)根據箱產量的頻率分布直方圖,對兩種養殖方法的優劣進行比較.
附:
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
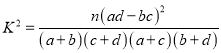
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知集合A={x|m+1≤x≤2m﹣1},B={x|x<﹣2或x>5}
(1)若AB,求實數m的取值范圍的集合;
(2)若A∩B=,求實數m的取值范圍的集合.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知集合A=[2,log2t],集合B={x|y= ![]() },
},
(1)對于區間[a,b],定義此區間的“長度”為b﹣a,若A的區間“長度”為3,試求實數t的值.
(2)若AB,試求實數t的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com