【題目】已知圓的方程為x2+y2﹣6x=0，過點（1，2）的該圓的三條弦的長a1 ， a2 ， a3構成等差數列，則數列a1 ， a2 ， a3的公差的最大值是 ．
科目：高中數學 來源： 題型：
【題目】袋中有6個編號不同的黑球和3個編號不同的白球，這9個球的大小及質地都相同，現從該袋中隨機摸取3個球，則這三個球中恰有兩個黑球和一個白球的方法總數是 ， 設摸取的這三個球中所含的黑球數為X，則P（X=k）取最大值時，k的值為 ．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在直角梯形ABCD中，AB⊥AD，AD∥BC，AB=BC=2AD=2，E，F分別為BC，CD的中點，以A為圓心，AD為半徑的半圓分別交BA及其延長線于點M，N，點P在 
上運動（如圖）．若 
，其中λ，μ∈R，則2λ﹣5μ的取值范圍是（ ） 
A.[﹣2，2]
B.
C.
D.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數f（x）=alnx+b（a，b∈R），曲線f（x）在x=1處的切線方程為x﹣y﹣1=0．
（Ⅰ）求a，b的值；
（Ⅱ）證明： 
；
（Ⅲ）已知滿足xlnx=1的常數為k．令函數g（x）=mex+f（x）（其中e是自然對數的底數，e=2.71828…），若x=x0是g（x）的極值點，且g（x）≤0恒成立，求實數m的取值范圍．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知m≠0，向量 
=（m，3m），向量 
=（m+1，6），集合A={x|（x﹣m2）（x+m﹣2）=0}．
（1）判斷“ ∥ ”是“| |= 
”的什么條件
（2）設命題p：若 ⊥ ，則m=﹣19，命題q：若集合A的子集個數為2，則m=1，判斷p∨q，p∧q，￢q的真假，并說明理由．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在△ABC中，角A，B，C所對的邊分別為a，b，c，且滿足acosB=bcosA．
（1）判斷△ABC的形狀；
（2）求sin（2A+ 
）﹣2cos2B的取值范圍．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】秦九韶是我國南宋時期的數學家，普州（現四川省安岳縣）人，他在所著的《數書九章》中提出的多項式求值的秦九韶算法，至今仍是比較先進的算法．如圖的程序框圖給出了利用秦九韶算法求某多項式值的一個實例，若輸入x的值為2，則輸出的v值為（ ）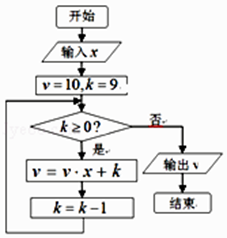 
A.9×210﹣2
B.9×210+2
C.9×211+2
D.9×211﹣2
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在直角坐標系xOy中，曲線C1的參數方程為 
（φ為參數），以原點O為極點，x軸的正半軸為極軸建立極坐標系，曲線C2的極坐標方程為ρ=4sinθ
（Ⅰ）求曲線C1的普通方程和C2的直角坐標方程；
（Ⅱ）已知曲線C3的極坐標方程為θ=α，0＜α＜π，ρ∈R，點A是曲線C3與C1的交點，點B是曲線C3與C2的交點，且A，B均異于原點O，且|AB|=4 
，求實數a的值．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
