
【題目】已知橢圓C的中心在原點,焦點在x軸上,D(0,2)為橢圓C短軸的一個端點,F為橢圓C的右焦點,線段DF的延長線與橢圓C相交于點E,且|DF|=3|EF|.
(1)求橢圓C的標(biāo)準(zhǔn)方程;
(2)設(shè)直線l與橢圓C相交于A,B兩點,O為坐標(biāo)原點,若直線OA與OB的斜率之積為-![]() ,求
,求![]() 的取值范圍.
的取值范圍.
【答案】(1)![]() +
+![]() =1(2)[-1,0)∪(0,1].
=1(2)[-1,0)∪(0,1].
【解析】
(1)先由條件得b,再根據(jù)條件得E坐標(biāo),代入橢圓方程解得a2(2)先設(shè)A,B兩點坐標(biāo),化簡條件得y1y2=![]() x1x2,再代入化簡
x1x2,再代入化簡![]() =
=![]() x1x2,聯(lián)立直線方程與橢圓方程,解得x1,x2,最后根據(jù)基本不等式求最值,解得取值范圍.
x1x2,聯(lián)立直線方程與橢圓方程,解得x1,x2,最后根據(jù)基本不等式求最值,解得取值范圍.
解:(1)設(shè)橢圓的方程為![]() +
+![]() =1,(a>b>0),右焦點F(c,0),
=1,(a>b>0),右焦點F(c,0),
∵D(0,2)為橢圓C短軸的一個端點,
∴b=2,
∵|DF|=3|EF|,
∴E(![]() ,-
,-![]() ),
),
∴![]() +
+![]() =1,即a2=2c2,
=1,即a2=2c2,
又c2=a2-4,
∴a2=2(a2-4),
解得a2=8,
故橢圓方程為![]() +
+![]() =1.
=1.
(2)∵kOAkOB=![]() <0,設(shè)kOA=k≠0,則kOB=
<0,設(shè)kOA=k≠0,則kOB=![]() ,
,
設(shè)A(x1,y1),B(x2,y2),
∴![]()
![]() =
=![]() ,
,
即y1y2=![]() x1x2,
x1x2,
∴![]()
![]() =x1x2+y1y2=
=x1x2+y1y2=![]() x1x2,
x1x2,
由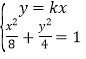 ,消y可得x2+2k2x2=8,即x12=
,消y可得x2+2k2x2=8,即x12=![]() ,
,
同理x22=![]() =
=![]() ,
,
∴x12x22=![]() =
=![]() ≤
≤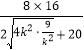 =
=![]() =4,
=4,
當(dāng)且僅當(dāng)4k2=![]() ,即k=±
,即k=±![]() 時取等號,
時取等號,
∴-2≤x1x2≤2,且x1x2≠0,
∴-1≤t≤1,且t≠0,
故![]() 的取值范圍為[-1,0)∪(0,1].
的取值范圍為[-1,0)∪(0,1].


 新課標(biāo)階梯閱讀訓(xùn)練系列答案
新課標(biāo)階梯閱讀訓(xùn)練系列答案科目:高中數(shù)學(xué) 來源: 題型:
【題目】從甲、乙兩種樹苗中各抽測了10株樹苗的高度,其莖葉圖如圖.根據(jù)莖葉圖,下列描述正確的是( )
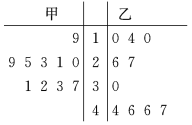
A.甲種樹苗的平均高度大于乙種樹苗的平均高度,且甲種樹苗比乙種樹苗長得整齊
B.甲種樹苗的平均高度大于乙種樹苗的平均高度,但乙種樹苗比甲種樹苗長得整齊
C.乙種樹苗的平均高度大于甲種樹苗的平均高度,且乙種樹苗比甲種樹苗長得整齊
D.乙種樹苗的平均高度大于甲種樹苗的平均高度,但甲種樹苗比乙種樹苗長得整齊
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知橢圓![]() :
:![]() 的短軸端點為
的短軸端點為![]() ,
,![]() ,點
,點![]() 是橢圓
是橢圓![]() 上的動點,且不與
上的動點,且不與![]() ,
,![]() 重合,點
重合,點![]() 滿足
滿足![]() ,
,![]() .
.

(Ⅰ)求動點![]() 的軌跡方程;
的軌跡方程;
(Ⅱ)求四邊形![]() 面積的最大值.
面積的最大值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】宋元時期數(shù)學(xué)名著《算學(xué)啟蒙》中有關(guān)于“松竹并生”的問題:松長五尺,竹長兩尺,松日自半,竹日自倍,松竹何日而長等.如圖是源于其思想的一個程序框圖,若輸入![]() ,
,![]() ,則輸出的
,則輸出的![]() 等于( )
等于( )
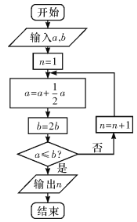
A. 3B. 4C. 5D. 6
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,在直四棱柱![]() 中,
中,![]()
![]()
![]()
![]() ,
,![]()
![]()
![]() :
:
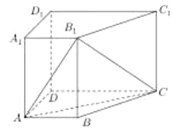
(1)求證:![]() 平面
平面![]() ;
;
(2)現(xiàn)將與四棱柱![]() 形狀和大小完全相同的兩個四棱柱拼成一個新的四棱柱,規(guī)定:若拼成的新四棱柱形狀和大小完全相同,則視為同一種拼接方案,問共有幾種不同的拼接方案?在這些拼接成的新四棱柱中,記其中最小的表面積為
形狀和大小完全相同的兩個四棱柱拼成一個新的四棱柱,規(guī)定:若拼成的新四棱柱形狀和大小完全相同,則視為同一種拼接方案,問共有幾種不同的拼接方案?在這些拼接成的新四棱柱中,記其中最小的表面積為![]() ,寫出
,寫出![]() 的解析式;(直接寫出答案,不必說明理由)
的解析式;(直接寫出答案,不必說明理由)
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】在平面直角坐標(biāo)系![]() 中,已知橢圓
中,已知橢圓![]() 過點
過點![]() ,且離心率
,且離心率![]() .
.
(1)求橢圓![]() 的方程;
的方程;
(2)直線![]() 的斜率為
的斜率為![]() ,直線
,直線![]() 與橢圓
與橢圓![]() 交于
交于![]() 、
、![]() 兩點,求
兩點,求![]() 的面積的最大值.
的面積的最大值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】橢圓![]() 的左、右焦點分別為
的左、右焦點分別為![]() ,右頂點為A,上頂點為B,且滿足向量
,右頂點為A,上頂點為B,且滿足向量![]() 。
。
(1)若![]() ,求橢圓的標(biāo)準(zhǔn)方程;
,求橢圓的標(biāo)準(zhǔn)方程;
(2)設(shè)![]() 為橢圓上異于頂點的點,以線段PB為直徑的圓經(jīng)過F1,問是否存在過F2的直線與該圓相切?若存在,求出其斜率;若不存在,說明理由。
為橢圓上異于頂點的點,以線段PB為直徑的圓經(jīng)過F1,問是否存在過F2的直線與該圓相切?若存在,求出其斜率;若不存在,說明理由。
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com