
【題目】如圖,在直四棱柱![]() 中,
中,![]()
![]()
![]()
![]() ,
,![]()
![]()
![]() :
:
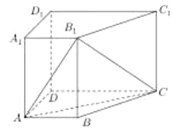
(1)求證:![]() 平面
平面![]() ;
;
(2)現將與四棱柱![]() 形狀和大小完全相同的兩個四棱柱拼成一個新的四棱柱,規定:若拼成的新四棱柱形狀和大小完全相同,則視為同一種拼接方案,問共有幾種不同的拼接方案?在這些拼接成的新四棱柱中,記其中最小的表面積為
形狀和大小完全相同的兩個四棱柱拼成一個新的四棱柱,規定:若拼成的新四棱柱形狀和大小完全相同,則視為同一種拼接方案,問共有幾種不同的拼接方案?在這些拼接成的新四棱柱中,記其中最小的表面積為![]() ,寫出
,寫出![]() 的解析式;(直接寫出答案,不必說明理由)
的解析式;(直接寫出答案,不必說明理由)
【答案】(1)詳見解析:(2)4種不同的拼接方案,f(k)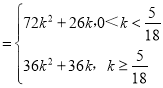
【解析】
(1)取DC的中點E,連接BE,可證明四邊形ABED是平行四邊形,再利用勾股定理的逆定理可得BE⊥CD,即CD⊥AD,又側棱AA1⊥底面ABCD,可得AA1⊥DC,利用線面垂直的判定定理即可證明.
(2)由題意可與左右平面ADD1A1,BCC1B1,上或下面ABCD,A1B1C1D1拼接得到方案,新四棱柱共有此4種不同方案.通過比較即可得出f(k).
(1)證明:取DC的中點E,連接BE,∵AB∥ED,AB=ED=3k,
∴四邊形ABED是平行四邊形,
∴BE∥AD,且BE=AD=4k,∴BE2+EC2=(4k)2+(3k)2=(5k)2=BC2,∴∠BEC=90°,∴BE⊥CD,
又∵BE∥AD,∴CD⊥AD.
∵側棱AA1⊥底面ABCD,∴AA1⊥CD,
∵AA1∩AD=A,∴CD⊥平面ADD1A1.
(2)由題意可與左右平面ADD1A1,BCC1B1,上或下面ABCD,A1B1C1D1拼接得到方案新四棱柱共有此4種不同方案.
通過比較即可得出f(k)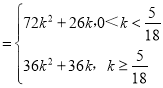 .
.


 學而優暑期銜接南京大學出版社系列答案
學而優暑期銜接南京大學出版社系列答案 Happy holiday歡樂假期暑假作業廣東人民出版社系列答案
Happy holiday歡樂假期暑假作業廣東人民出版社系列答案科目:高中數學 來源: 題型:
【題目】如圖,在三棱錐![]() 中,已知
中,已知![]() ,
,![]() ,平面
,平面![]() 平面
平面![]() ,點
,點![]() 分別是
分別是![]() 的中點,
的中點,![]() ,連接
,連接![]() .
.
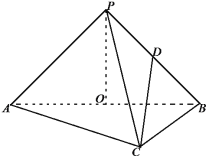
(1)若![]() ,并異面直線
,并異面直線![]() 與
與![]() 所成角的余弦值的大小;
所成角的余弦值的大小;
(2)若二面角![]() 的余弦值的大小為
的余弦值的大小為![]() ,求
,求![]() 的長.
的長.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知點P(2,2),圓![]() ,過點P的動直線l與圓C交于A,B兩點,線段AB的中點為M,O為坐標原點.
,過點P的動直線l與圓C交于A,B兩點,線段AB的中點為M,O為坐標原點.
(1)求點M的軌跡方程;
(2)當|OP|=|OM|時,求l的方程及△POM的面積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的離心率為
的離心率為![]() ,若橢圓上的點與兩個焦點構成的三角形中,面積最大為1.
,若橢圓上的點與兩個焦點構成的三角形中,面積最大為1.
(1)求橢圓的標準方程;
(2)設直線![]() 與橢圓的交于
與橢圓的交于![]() 兩點,
兩點,![]() 為坐標原點,且
為坐標原點,且![]() ,證明:直線
,證明:直線![]() 與圓
與圓![]() 相切.
相切.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓C的中心在原點,焦點在x軸上,D(0,2)為橢圓C短軸的一個端點,F為橢圓C的右焦點,線段DF的延長線與橢圓C相交于點E,且|DF|=3|EF|.
(1)求橢圓C的標準方程;
(2)設直線l與橢圓C相交于A,B兩點,O為坐標原點,若直線OA與OB的斜率之積為-![]() ,求
,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某射手每次射擊擊中目標的概率是![]() ,且各次射擊的結果互不影響.
,且各次射擊的結果互不影響.
(Ⅰ)假設這名射手射擊![]() 次,求有
次,求有![]() 次連續擊中目標,另外
次連續擊中目標,另外![]() 次未擊中目標的概率;
次未擊中目標的概率;
(Ⅱ)假設這名射手射擊![]() 次,記隨機變量
次,記隨機變量![]() 為射手擊中目標的次數,求
為射手擊中目標的次數,求![]() 的分布列及數學期望.
的分布列及數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2019年的天貓“雙11”交易金額又創新高,達到2684億元,物流爆增.某機構為了了解網購者對收到快遞的滿意度進行調查,對某市5000名網購者發出滿意度調查評分表,收集并隨機抽取了200名網購者的調查評分(評分在70~100分之間),其頻率分布直方圖如圖,評分在95分及以上確定為“非常滿意”.
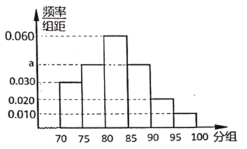
(1)求![]() 的值;
的值;
(2)以樣本的頻率作概率,試估計本次調查的網購者中“非常滿意”的人數;
(3)按分層抽樣的方法,從評分在90分及以上的網購者中抽取6人,再從這6人中隨機地選取2人,求至少選到一個“非常滿意”的概率.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com