
【題目】如圖,在平面直角坐標系![]() 中,己知拋物線
中,己知拋物線![]() 的焦點為
的焦點為![]() ,點
,點![]() 是第一象限內拋物線
是第一象限內拋物線![]() 上的一點,點
上的一點,點![]() 的坐標為
的坐標為![]()
(1)若![]() ,求點
,求點![]() 的坐標;
的坐標;
(2)若![]() 為等腰直角三角形,且
為等腰直角三角形,且![]() ,求點
,求點![]() 的坐標;
的坐標;
(3)弦![]() 經過點
經過點![]() ,過弦
,過弦![]() 上一點
上一點![]() 作直線
作直線![]() 的垂線,垂足為點
的垂線,垂足為點![]() ,求證:“直線
,求證:“直線![]() 與拋物線相切”的一個充要條件是“
與拋物線相切”的一個充要條件是“![]() 為弦
為弦![]() 的中點”.
的中點”.
【答案】(1)![]() (2)
(2)![]() (3)證明見解析
(3)證明見解析
【解析】
(1)因為點![]() 是第一象限內拋物線
是第一象限內拋物線![]() 上的一點,且
上的一點,且![]() ,設
,設![]() ,
,
則  即可求得答案;
即可求得答案;
(2)設![]() ,由
,由![]() ,
,![]() ,可得:
,可得:![]() ,
,![]() ,因為
,因為 ![]() ,可得
,可得![]() ,結合已知,即可求得答案;
,結合已知,即可求得答案;
(3)因為![]() 過點
過點![]() ,設
,設![]() 為:
為:![]() ,點
,點![]() ,點
,點![]() ,其
,其![]() 中點
中點![]() ,可得:
,可得:![]() ,聯立直線與拋物線得
,聯立直線與拋物線得![]() ,結合已知條件,根據充要條件定義,即可求得答案.
,結合已知條件,根據充要條件定義,即可求得答案.
(1)![]() 點
點![]() 是第一象限內拋物線
是第一象限內拋物線![]() 上的一點,且
上的一點,且![]()
設![]() ,
,
則 
解得: ,即
,即![]() .
.
(2)設![]() ,由
,由![]() ,
,![]()
可得:![]() ,
,![]()
![]()
![]()
![]()
![]()
![]()
![]() ①
①
又![]()
![]() 等腰,得
等腰,得![]() 點在
點在![]() 軸投影為
軸投影為![]() 、
、![]() 中點,即:
中點,即:![]() .
.
將![]() ,
,![]() 代入①得:
代入①得:![]() ,
,![]() (舍去)
(舍去)
![]()
![]() 點坐標為
點坐標為![]() .
.
(3)![]()
![]() 過點
過點![]()
設![]() 為:
為:![]() ,點
,點![]() ,點
,點![]() ,其
,其![]() 中點
中點![]() ,
,
可得:![]()
聯立直線與拋物線得![]() ,消掉
,消掉![]()
可得:![]()
根據韋達定理可得:![]()
![]()
![]()
設點![]() 處拋物線得切線為
處拋物線得切線為![]()
聯立直線與拋物線得: ,消掉
,消掉![]()
可得:![]()
![]()
![]()
![]()
 ,可得:
,可得:![]()
![]() 過
過![]() 處切線方程為
處切線方程為![]()
化簡得![]()
求切線![]() 與直線
與直線![]() 得交點
得交點![]()
可得![]()
![]()
![]() 軸,
軸,
![]() 與
與![]() 相切時,
相切時,![]() 為
為![]() 中點
中點
![]() 以上各步驟,均可逆
以上各步驟,均可逆
![]() “直線
“直線![]() 與拋物線相切”的一個充要條件是“
與拋物線相切”的一個充要條件是“![]() 為弦
為弦![]() 的中點”.
的中點”.


科目:高中數學 來源: 題型:
【題目】有著“中國碳谷”之稱的安徽省淮北市,名優特產眾多,其中“塔山石榴”因其青皮軟籽、籽粒飽滿、晶瑩剔透、汁多味甘而享譽天下.現調查表明,石榴的甜度與海拔、日照時長、晝夜溫差有著極強的相關性,分別用![]() 表示石榴甜度與海拔、日照時長、溫差的相關程度,并對它們進行量化:0表示一般,1表示良,2表示優,再用綜合指標
表示石榴甜度與海拔、日照時長、溫差的相關程度,并對它們進行量化:0表示一般,1表示良,2表示優,再用綜合指標![]() 的值評定石榴的等級,若
的值評定石榴的等級,若![]() 則為一級;若
則為一級;若![]() 則為二級;若
則為二級;若![]() 則為三級.
則為三級.![]() 近年來,周邊各地市也開始發展石榴的種植,為了了解目前石榴在周邊地市的種植情況,研究人員從不同地市隨機抽取了12個石榴種植園,得到如下結果:
近年來,周邊各地市也開始發展石榴的種植,為了了解目前石榴在周邊地市的種植情況,研究人員從不同地市隨機抽取了12個石榴種植園,得到如下結果:
種植園編號 | A | B | C | D | E | F |
|
|
|
|
|
|
|
種植園編號 | G | H | I | J | K | L |
|
|
|
|
|
|
|
(1)若有石榴種植園120個,估計等級為一級的石榴種植園的數量;
(2)在所取樣本的二級和三級石榴種植園中任取2個,![]() 表示取到三級石榴種植園的數量,求隨機變量
表示取到三級石榴種植園的數量,求隨機變量![]() 的分布列及數學期望.
的分布列及數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]()
![]() 經過點
經過點![]() ,離心率為
,離心率為![]() ,過點
,過點![]() 的直線
的直線![]() 與橢圓
與橢圓![]() 交于不同的兩點
交于不同的兩點![]() ,
,
(1)求橢圓![]() 的方程;
的方程;
(2)求![]() 的取值范圍;
的取值范圍;
(3)設直線![]() 和
和![]() 的斜率分別為
的斜率分別為![]() 和
和![]() ,求證:
,求證:![]() 為定值.
為定值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】經過多年的努力,炎陵黃桃在國內乃至國際上逐漸打開了銷路,成為炎陵部分農民脫貧致富的好產品.為了更好地銷售,現從某村的黃桃樹上隨機摘下了100個黃桃進行測重,其質量分布在區間![]() 內(單位:克),統計質量的數據作出其頻率分布直方圖如圖所示:
內(單位:克),統計質量的數據作出其頻率分布直方圖如圖所示:
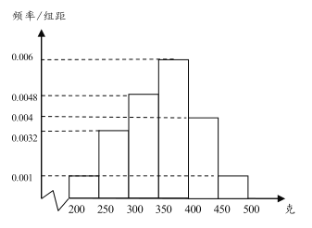
(1)按分層抽樣的方法從質量落在![]() ,
,![]() 的黃桃中隨機抽取5個,再從這5個黃桃中隨機抽2個,求這2個黃桃質量至少有一個不小于400克的概率;
的黃桃中隨機抽取5個,再從這5個黃桃中隨機抽2個,求這2個黃桃質量至少有一個不小于400克的概率;
(2)以各組數據的中間數值代表這組數據的平均水平,以頻率代表概率,已知該村的黃桃樹上大約還有100000個黃桃待出售,某電商提出兩種收購方案:
A.所有黃桃均以20元/千克收購;
B.低于350克的黃桃以5元/個收購,高于或等于350克的以9元/個收購.
請你通過計算為該村選擇收益最好的方案.
(參考數據:![]() )
)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com