
【題目】已知函數![]() ,其中
,其中![]() .
.
(Ⅰ)當![]() 時,求曲線
時,求曲線![]() 在點
在點![]() 處的切線方程;
處的切線方程;
(Ⅱ)求證: 當![]() 時,
時,![]() .
.
【答案】(Ⅰ)y=2e (Ⅱ)見證明
【解析】
(Ⅰ)求出導函數,求出切點坐標,切線的斜率,然后求解曲線y=f(x)在(﹣1,f(﹣1))處的切線方程;
(Ⅱ)法一:![]() ,令f'(x)=0,求出極值點,判斷導函數的符號,得到函數的單調性,求出函數的最小值,只需證明
,令f'(x)=0,求出極值點,判斷導函數的符號,得到函數的單調性,求出函數的最小值,只需證明![]() ,
,![]() ,
,![]() ,設
,設![]() ,其中x>2,利用導函數轉化求解即可;
,其中x>2,利用導函數轉化求解即可;
法二:設![]() ,其中x>0,
,其中x>0,![]() ,推出F(x)在區間(0,2)上單調遞減,在(2,+∞)上單調遞增,所以函數F(x)在x=2時取得最小值
,推出F(x)在區間(0,2)上單調遞減,在(2,+∞)上單調遞增,所以函數F(x)在x=2時取得最小值![]() ,而
,而![]() ,推出結果即可;
,推出結果即可;
法三:因為“對任意的x>0,![]() ”等價于“對任意的x>0,
”等價于“對任意的x>0,![]() ”,只需證“x>0時,2ex+e(a﹣x2)>0”,設g(x)=2ex+e(a﹣x2),其中x≥0,g'(x)=2ex﹣2ex,設h(x)=g'(x),h'(x)=2ex﹣2e,求出函數的極小值,通過g(x)在(0,+∞)上單調遞增,得g(x)>g(0),轉化證明即可.
”,只需證“x>0時,2ex+e(a﹣x2)>0”,設g(x)=2ex+e(a﹣x2),其中x≥0,g'(x)=2ex﹣2ex,設h(x)=g'(x),h'(x)=2ex﹣2e,求出函數的極小值,通過g(x)在(0,+∞)上單調遞增,得g(x)>g(0),轉化證明即可.
(Ⅰ)因為![]()
所以![]()
當![]() 時,
時,![]()
所以![]() ,而
,而![]()
曲線![]() 在
在![]() 處的切線方程為
處的切線方程為![]()
(Ⅱ)法一:
因為![]() ,令
,令![]()
得![]()
顯然當![]() 時,
時,![]()
所以![]() ,
,![]() ,
,![]() 在區間
在區間![]() 上的變化情況如下表:
上的變化情況如下表:
|
|
|
|
|
| 0 |
|
|
| 極小值 |
|
所以![]() 在區間
在區間![]() 上單調遞減,在
上單調遞減,在![]() 單調遞增,
單調遞增,
所以![]() 在
在![]() 上的最小值為
上的最小值為![]() ,所以只需證明
,所以只需證明![]()
因為![]() ,所以
,所以![]()
設![]() ,其中
,其中![]()
所以![]()
當![]() 時,
時,![]() ,所以
,所以![]() 在區間
在區間![]() 單調遞增,
單調遞增,
因為 ![]() ,所以
,所以![]() ,問題得證
,問題得證
法二:
因為![]() ,所以當
,所以當![]() 時,
時,![]()
設![]() ,其中
,其中![]()
所以![]()
所以![]() ,
,![]() ,
,![]() 的變化情況如下表:
的變化情況如下表:
|
|
|
|
|
| 0 |
|
|
| 極小值 |
|
所以![]() 在區間
在區間![]() 上單調遞減,在
上單調遞減,在![]() 上單調遞增,
上單調遞增,
所以函數![]() 在
在![]() 時取得最小值
時取得最小值![]() ,而
,而![]()
所以![]() 時
時![]()
所以![]() ,問題得證
,問題得證
法三:
因為“對任意的![]() ,
,![]() ”等價于“對任意的
”等價于“對任意的![]() ,
,![]() ”
”
即“![]() ,
,![]() ”,故只需證“
”,故只需證“![]() 時,
時,![]() ”
”
設![]() ,其中
,其中![]()
所以![]()
設![]() ,
,![]() ,
,
令![]() ,得
,得![]()
所以![]() ,
,![]() ,
,![]() 的變化情況如下表:
的變化情況如下表:
|
|
|
|
|
| 0 |
|
|
| 極小值 |
|
所以![]() 在
在![]() 處取得極小值,而
處取得極小值,而![]()
所以![]()
所以![]() 時,
時,![]() ,所以
,所以![]() 在
在![]() 上單調遞增,得
上單調遞增,得![]()
而![]() ,所以
,所以![]() 問題得證
問題得證


科目:高中數學 來源: 題型:
【題目】函數f(x)=Asin(ωx+φ) ![]() 的部分圖象如圖所示.
的部分圖象如圖所示.

(1)求函數y=f(x)的解析式;
(2)求f(x)的單調減區間
(3)當![]() 時,求f(x)的取值范圍.
時,求f(x)的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知點![]() 和橢圓
和橢圓![]() . 直線
. 直線![]() 與橢圓
與橢圓![]() 交于不同的兩點
交于不同的兩點![]() .
.
(Ⅰ) 求橢圓![]() 的離心率;
的離心率;
(Ⅱ) 當![]() 時,求
時,求![]() 的面積;
的面積;
(Ⅲ)設直線![]() 與橢圓
與橢圓![]() 的另一個交點為
的另一個交點為![]() ,當
,當![]() 為
為![]() 中點時,求
中點時,求![]() 的值 .
的值 .
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】甲、乙兩人做游戲,下列游戲不公平的是( )
A.拋擲一枚骰子,向上的點數為奇數則甲獲勝,向上的點數為偶數則乙獲勝
B.甲、乙兩人各寫一個數字1或2,如果兩人寫的數字相同甲獲勝,否則乙獲勝
C.從一副不含大小王的撲克牌中抽一張,撲克牌是紅色的則甲獲勝,撲克牌是黑色的則乙獲勝
D.同時拋擲兩枚硬幣,恰有一枚正面向上則甲獲勝,兩枚都正面向上則乙獲勝
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某校的一個社會實踐調查小組,在對該校學生的良好“用眼習慣”的調查中,隨機發放了120分問卷.
對收回的100份有效問卷進行統計,得到如下2×2列聯表:
做不到科學用眼 | 能做到科學用眼 | 合計 | |
男 | 45 |
|
|
女 |
| 15 |
|
合計 |
|
| 100 |
(1)求上表中的x
(2)若在犯錯誤的概率不超過P的前提下認為良好“用眼習慣”與性別有關,那么根據臨界值表,最精確的P的值應為多少?
附:獨立性檢驗統計量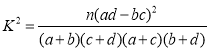 ,其中
,其中![]() .
.
獨立性檢驗臨界值表:
| 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
| 1.323 | 2.072 | 2.706 | 3.840 | 5.024 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某工廠生產某種型號的農機具零配件,為了預測今年7月份該型號農機具零配件的市場需求量,以合理安排生產,工廠對本年度1月份至6月份該型號農機具零配件的銷售量及銷售單價進行了調查,銷售單價![]() (單位:元)和銷售量
(單位:元)和銷售量![]() (單位:千件)之間的6組數據如下表所示:
(單位:千件)之間的6組數據如下表所示:
月份 | 1 | 2 | 3 | 4 | 5 | 6 |
銷售單價 | 11.1 | 9.1 | 9.4 | 10.2 | 8.8 | 11.4 |
銷售量 | 2.5 | 3.1 | 3 | 2.8 | 3.2 | 2.4 |
(1)根據1至6月份的數據,求![]() 關于
關于![]() 的線性回歸方程(系數精確到0.01);
的線性回歸方程(系數精確到0.01);
(2)結合(1)中的線性回歸方程,假設該型號農機具零配件的生產成本為每件3元,那么工廠如何制定7月份的銷售單價,才能使該月利潤達到最大?(計算結果精確到0.1)
參考公式:回歸直線方程![]() ,
,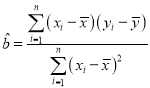
參考數據:![]() ,
,![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下表為![]() 年至
年至![]() 年某百貨零售企業的線下銷售額(單位:萬元),其中年份代碼
年某百貨零售企業的線下銷售額(單位:萬元),其中年份代碼![]() 年份
年份![]() .
.
年份代碼 |
|
|
|
|
線下銷售額 |
|
|
|
|
(1)已知![]() 與
與![]() 具有線性相關關系,求
具有線性相關關系,求![]() 關于
關于![]() 的線性回歸方程,并預測
的線性回歸方程,并預測![]() 年該百貨零售企業的線下銷售額;
年該百貨零售企業的線下銷售額;
(2)隨著網絡購物的飛速發展,有不少顧客對該百貨零售企業的線下銷售額持續增長表示懷疑,某調查平臺為了解顧客對該百貨零售企業的線下銷售額持續增長的看法,隨機調查了![]() 位男顧客、
位男顧客、![]() 位女顧客(每位顧客從“持樂觀態度”和“持不樂觀態度”中任選一種),其中對該百貨零售企業的線下銷售額持續增長持樂觀態度的男顧客有
位女顧客(每位顧客從“持樂觀態度”和“持不樂觀態度”中任選一種),其中對該百貨零售企業的線下銷售額持續增長持樂觀態度的男顧客有![]() 人、女顧客有
人、女顧客有![]() 人,能否在犯錯誤的概率不超過
人,能否在犯錯誤的概率不超過![]() 的前提下認為對該百貨零售企業的線下銷售額持續增長所持的態度與性別有關?
的前提下認為對該百貨零售企業的線下銷售額持續增長所持的態度與性別有關?
參考公式及數據: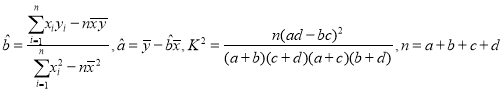 .
.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com