
【題目】已知在函數(shù)![]() (
(![]() )的所有切線中,有且僅有一條切線
)的所有切線中,有且僅有一條切線![]() 與直線
與直線![]() 垂直.
垂直.
(1)求![]() 的值和切線
的值和切線![]() 的方程;
的方程;
(2)設(shè)曲線![]() 在任一點(diǎn)處的切線傾斜角為
在任一點(diǎn)處的切線傾斜角為![]() ,求
,求![]() 的取值范圍.
的取值范圍.
【答案】(1)![]() (2)
(2)![]() 或
或![]() .
.
【解析】試題分析:(1)由已知可得函數(shù)的導(dǎo)函數(shù),即切線斜率的函數(shù),因為在曲線![]() 的所有切線中,有且僅有一條切線
的所有切線中,有且僅有一條切線![]() 與直線
與直線![]() 垂直,所以導(dǎo)函數(shù)只有一個實(shí)根,進(jìn)而易得
垂直,所以導(dǎo)函數(shù)只有一個實(shí)根,進(jìn)而易得![]() 的值與切線
的值與切線![]() 的方程.(2)因為在曲線
的方程.(2)因為在曲線![]() 的所有切線中,有且僅有一條切線l與直線
的所有切線中,有且僅有一條切線l與直線![]() 垂直,顯然切線斜率
垂直,顯然切線斜率![]() 從而可以解出
從而可以解出![]() 的范圍.
的范圍.
試題解析:
(1)![]() ,由題意知,方程
,由題意知,方程![]() 有兩個相等的根,
有兩個相等的根,
∴![]() ,∴
,∴![]() .
.
此時方程![]() 化為
化為![]() ,得
,得![]() ,
,
解得切點(diǎn)的縱坐標(biāo)為![]() ,
,
∴切線![]() 的方程為
的方程為![]() ,即
,即![]() .
.
(2)設(shè)曲線![]() 上任一點(diǎn)
上任一點(diǎn)![]() 處的切線的斜率為
處的切線的斜率為![]() (由題意知
(由題意知![]() 存在),
存在),
則由(1)知![]() ,
,
∴由正切函數(shù)的單調(diào)性可得![]() 的取值范圍為
的取值范圍為![]() 或
或![]() .
.



| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
【題目】設(shè)函數(shù)fk(x)=xk+bx+c(k∈N* , b,c∈R),g(x)=logax(a>0,a≠1).
(1)若b+c=1,且fk(1)=g( ![]() ),求a的值;
),求a的值;
(2)若k=2,記函數(shù)fk(x)在[﹣1,1]上的最大值為M,最小值為m,求M﹣m≤4時的b的取值范圍;
(3)判斷是否存在大于1的實(shí)數(shù)a,使得對任意x1∈[a,2a],都有x2∈[a,a2]滿足等式:g(x1)+g(x2)=p,且滿足該等式的常數(shù)p的取值唯一?若存在,求出所有符合條件的a的值;若不存在,請說明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() .
.
(Ⅰ)若![]() ,證明:函數(shù)
,證明:函數(shù)![]() 是
是![]() 上的減函數(shù);
上的減函數(shù);
(Ⅱ)若曲線![]() 在點(diǎn)
在點(diǎn)![]() 處的切線與直線
處的切線與直線![]() 平行,求
平行,求![]() 的值;
的值;
(Ⅲ)若![]() ,證明:
,證明: ![]() (其中
(其中![]() …是自然對數(shù)的底數(shù)).
…是自然對數(shù)的底數(shù)).
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】橢圓與雙曲線有相同的焦點(diǎn)![]() ,
,![]() ,橢圓的一個短軸端點(diǎn)為
,橢圓的一個短軸端點(diǎn)為![]() ,直線
,直線![]() 與雙曲線的一條漸近線平行,若橢圓于雙曲線的離心率分別為
與雙曲線的一條漸近線平行,若橢圓于雙曲線的離心率分別為![]() ,
,![]() ,則
,則![]() 的最小值為__________.
的最小值為__________.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
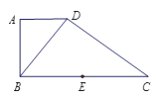
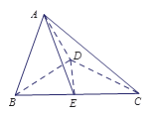
【題目】如圖,在直角梯形![]() 中,
中, ![]() //
// ![]() ,
, ![]() ⊥
⊥![]() ,
, ![]() ⊥
⊥![]() , 點(diǎn)
, 點(diǎn)![]() 是
是![]() 邊的中點(diǎn), 將△
邊的中點(diǎn), 將△![]() 沿
沿![]() 折起,使平面
折起,使平面![]() ⊥平面
⊥平面![]() ,連接
,連接![]() ,
, ![]() ,
, ![]() , 得到如
, 得到如
圖所示的空間幾何體.
(Ⅰ)求證: ![]() ⊥平面
⊥平面![]() ;
;
(Ⅱ)若![]() ,求點(diǎn)
,求點(diǎn)![]() 到平面
到平面![]() 的距離.
的距離.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某家庭進(jìn)行理財投資,根據(jù)長期收益率市場預(yù)測,投資債券等穩(wěn)健型產(chǎn)品的收益與投資額成正比,投資股票等風(fēng)險型產(chǎn)品的收益與投資額的算術(shù)平方根成正比.已知投資1萬元時兩類產(chǎn)品的收益分別為0.125萬元和0.5萬元(如圖). 
(1)分別寫出兩種產(chǎn)品的收益與投資額的函數(shù)關(guān)系式;
(2)該家庭現(xiàn)有20萬元資金,全部用于理財投資,問:怎么分配資金能使投資獲得最大收益,其最大收益是多少萬元?
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某地區(qū)擬建立一個藝術(shù)博物館,采取競標(biāo)的方式從多家建筑公司選取一家建筑公司,經(jīng)過層層篩選,甲、乙兩家建筑公司進(jìn)入最后的招標(biāo).現(xiàn)從建筑設(shè)計院聘請專家設(shè)計了一個招標(biāo)方案:兩家公司從![]() 個招標(biāo)問題中隨機(jī)抽取
個招標(biāo)問題中隨機(jī)抽取![]() 個問題,已知這
個問題,已知這![]() 個招標(biāo)問題中,甲公司可正確回答其中的
個招標(biāo)問題中,甲公司可正確回答其中的![]() 道題目,而乙公司能正確回答毎道題目的概率均為
道題目,而乙公司能正確回答毎道題目的概率均為![]() ,甲、乙兩家公司對每題的回答都是相互獨(dú)立,互不影響的.
,甲、乙兩家公司對每題的回答都是相互獨(dú)立,互不影響的.
(1)求甲、乙兩家公司共答對![]() 道題目的概率;
道題目的概率;
(2)請從期望和方差的角度分析,甲、乙兩家哪家公司競標(biāo)成功的可能性更大?
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知命題![]() :
: ![]() ,命題
,命題![]()
![]() .
.
(1)若命題![]() 為真命題,求實(shí)數(shù)
為真命題,求實(shí)數(shù)![]() 的取值范圍;
的取值范圍;
(2)若命題![]() 為真命題,求實(shí)數(shù)
為真命題,求實(shí)數(shù)![]() 的取值范圍;
的取值范圍;
(3)若命題“![]() ”為真命題,且命題“
”為真命題,且命題“![]() ”為假命題,求實(shí)數(shù)
”為假命題,求實(shí)數(shù)![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com