【題目】某家庭進行理財投資，根據長期收益率市場預測，投資債券等穩健型產品的收益與投資額成正比，投資股票等風險型產品的收益與投資額的算術平方根成正比．已知投資1萬元時兩類產品的收益分別為0.125萬元和0.5萬元（如圖）． 
（1）分別寫出兩種產品的收益與投資額的函數關系式；
（2）該家庭現有20萬元資金，全部用于理財投資，問：怎么分配資金能使投資獲得最大收益，其最大收益是多少萬元？
【答案】
（1）解：f（x）=k1x，g（x）= 
，
f（1）= 
=k1，g（1）=k2= 
，
∴f（x）= x（x≥0），g（x）= 
（x≥0）
（2）解：設：投資債券類產品x萬元，則股票類投資為20﹣x萬元．
y=f（x）+g（20﹣x）= 
（0≤x≤20）
令t= 
，則y= 
=﹣ 
．
所以當t=2，即x=16萬元時，收益最大，ymax=3萬元
【解析】（1）由投資債券等穩健型產品的收益與投資額成正比，投資股票等風險型產品的收益與投資額的算術平方根成正比，結合函數圖象，我們可以利用待定系數法來求兩種產品的收益與投資的函數關系；（2）由（1）的結論，我們設設投資債券類產品x萬元，則股票類投資為20﹣x萬元．這時可以構造出一個關于收益y的函數，然后利用求函數最大值的方法進行求解．
假期作業暑假成長樂園新疆青少年出版社系列答案科目：高中數學 來源： 題型：
【題目】設函數
.
（1）若
是函數
的極值點，1為函數
的一個零點，求函數
在
上的最小值.
（2）當
時，函數
與
軸在
內有兩個不同的交點，求
的取值范圍.（其中
是自然對數的底數）
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖所示，有兩個獨立的轉盤（
）、（
）．兩個圖中三個扇形區域的圓心角分別為
、
、
．用這兩個轉盤進行玩游戲，規則是：依次隨機轉動兩個轉盤再隨機停下（指針固定不會動，當指針恰好落在分界線時，則這次結果無效，重新開始），記轉盤（）指針所對的數為
，轉盤（）指針所對的數為
，（、
），求下列概率：
（1）
；
（2）
．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在一次運動會中甲、乙兩名射擊運動員決賽中各射擊十次的成績（環）如下：
（1）用莖葉圖表示甲、乙兩個人的成績；
（2）根據莖葉圖分析甲、乙兩人的成績；
（3）計算兩個樣本的平均數
和標準差
，并根據計算結果估計哪位運動員的成績比較穩定．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某農科所發現，一種作物的年收獲量 
（單位： 
）與它“相近”作物的株數 
具有線性相關關系(所謂兩株作物“相近”是指它們的直線距離不超過 
)，并分別記錄了相近作物的株數為 
時，該作物的年收獲量的相關數據如下：
|
|
|
|
|
|
|
|
|
|
|
|
|
|
（1）求該作物的年收獲量 
關于它“相近”作物的株數
的線性回歸方程；
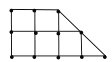
（2）農科所在如圖所示的直角梯形地塊的每個格點（指縱、橫直線的交叉點）處都種了一株該作物，圖中
每個小正方形的邊長均為 
，若從直角梯形地塊的邊界和內部各隨機選取一株該作物，求這兩株作物 “相
近”且年產量僅相差
的概率．
附：對于一組數據
，其回歸直線
的斜率和截距的最小二乘估
計分別為,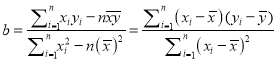 
, 
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】選修4
4：坐標系與參數方程
在直角坐標系
中，已知直線l1： 
（
， 
），拋物線C： 
（t為參數）．以原點
為極點， 
軸的非負半軸為極軸建立極坐標系．
（Ⅰ）求直線l1 和拋物線C的極坐標方程；
（Ⅱ）若直線l1 和拋物線C相交于點A（異于原點O），過原點作與l1垂直的直線l2，l2和拋物線C相交于點B（異于原點O），求△OAB的面積的最小值．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
