
已知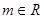 ,對
,對 :
: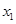 和
和 是方程
是方程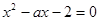 的兩個根,不等式
的兩個根,不等式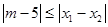 對任意實數
對任意實數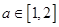 恒成立;
恒成立;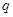 :函數
:函數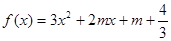 有兩個零點,求使“
有兩個零點,求使“ 且
且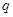 ”為真命題的實數的取值范圍。
”為真命題的實數的取值范圍。
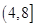
【解析】
試題分析:利用二次方程的韋達定理求出|x1-x2|,將不等式恒成立轉化為求函數的最值,求出命題p為真命題時m的范圍;利用二次方程有兩個不等根判別式大于0,求出命題Q為真命題時m的范圍;P且Q為真轉化為兩個命題全真,求出m的范圍.解:由題設x1+x2=a,x1x2=-2,∴|x1-x2|=
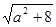 .當a∈[1,2]時,
.當a∈[1,2]時,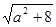 的最小值為3.要使|m-5|≤|x1-x2|對任意實數a∈[1,2]恒成立,只須|m-5|≤3,即2≤m≤8.由已知,得f(x)=3x2+2mx+m+
的最小值為3.要使|m-5|≤|x1-x2|對任意實數a∈[1,2]恒成立,只須|m-5|≤3,即2≤m≤8.由已知,得f(x)=3x2+2mx+m+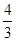 =0的判別式△=4m2-12(m+
=0的判別式△=4m2-12(m+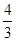 )=4m2-12m-16>0,得m<-1或m>4.綜上,要使“p且q”為真命題,只需P真Q真,即2≤m≤8,m<-1或m>4,解得實數m的取值范圍是(4,8].
)=4m2-12m-16>0,得m<-1或m>4.綜上,要使“p且q”為真命題,只需P真Q真,即2≤m≤8,m<-1或m>4,解得實數m的取值范圍是(4,8].
考點:二次方程的韋達定理
點評:本題考查二次方程的韋達定理、二次方程有根的判斷、復合命題的真假與構成其簡單命題的真假的關系.


科目:高中數學 來源: 題型:
| 1 |
| 3 |
| x | 2 k |
查看答案和解析>>
科目:高中數學 來源: 題型:
| 1 | 3 |
查看答案和解析>>
科目:高中數學 來源:2013屆江西省高二下學期第二次月考文科數學試卷(解析版) 題型:解答題
:已知 ,對
,對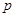 :
: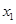 和
和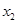 是方程
是方程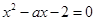 的兩個根,不等式
的兩個根,不等式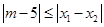 對任意實數
對任意實數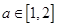 恒成立;
恒成立;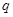 :函數
:函數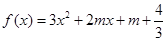 有兩個零點,求使“
有兩個零點,求使“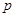 且
且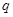 ”為真命題的實數的取值范圍。
”為真命題的實數的取值范圍。
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com