
【題目】已知雙曲線![]() 的左、右頂點分別為
的左、右頂點分別為![]() ,直線
,直線![]() 與雙曲線交于
與雙曲線交于![]() ,直線
,直線![]() 交直線
交直線![]() 于點
于點![]() .
.
(1)求點![]() 的軌跡方程;
的軌跡方程;
(2)若點![]() 的軌跡與矩形
的軌跡與矩形![]() 的四條邊都相切,探究矩形
的四條邊都相切,探究矩形![]() 對角線長是否為定值,若是,求出此值;若不是,說明理由.
對角線長是否為定值,若是,求出此值;若不是,說明理由.

【答案】(1) ![]() ;(2)見解析.
;(2)見解析.
【解析】試題分析:(1)利用交軌法,求出點![]() 的軌跡方程;(2) 設(shè)點
的軌跡方程;(2) 設(shè)點![]() ,過點
,過點![]() 作橢圓的切線,則切線的斜率存在且不為0,設(shè)斜率為
作橢圓的切線,則切線的斜率存在且不為0,設(shè)斜率為![]() ,則切線方程為
,則切線方程為![]() ,
,
代入到橢圓方程整理,得![]() .由
.由![]() 得到
得到
![]() ,這個關(guān)于
,這個關(guān)于![]() 的一元二次方程的兩根即為
的一元二次方程的兩根即為![]() 與
與![]() ,
,
由![]() ,可知
,可知![]() ,即
,即![]() ,即點
,即點![]() 為矩形
為矩形![]() 外接圓的圓心,其中
外接圓的圓心,其中![]() 為直徑,大小為
為直徑,大小為![]() ,故矩形
,故矩形![]() 對角線長為定值
對角線長為定值![]() .
.
試題解析:
(1)設(shè)點![]() ,
, ![]() ,
, ![]() ,其中
,其中![]() .
.
由題意,得![]() ,
, ![]() .
.
由![]() ,①
,①
![]() ,②
,②
兩式相乘得![]() .
.
∵![]() ,
,
∴![]() ,
,
代入上式得
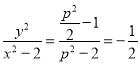
![]() ,
,
由①與![]() ,得
,得![]() ,
,
①÷②,得![]() .
.
故點![]() 的軌跡方程為
的軌跡方程為![]() .
.
(2)設(shè)點![]() ,過點
,過點![]() 作橢圓的切線,
作橢圓的切線,
則切線的斜率存在且不為0,設(shè)斜率為![]() ,
,
則切線方程為![]() ,
,
代入到橢圓方程整理,
得![]() .
.
![]()
![]() ,
,
即![]() .
.
這個關(guān)于![]() 的一元二次方程的兩根即為
的一元二次方程的兩根即為![]() 與
與![]() ,
,
由![]() ,
,
得![]() .
.
設(shè)![]() 為坐標(biāo)原點,故可知
為坐標(biāo)原點,故可知![]() ,
,
同理,得![]() ,
,
即點![]() 為矩形
為矩形![]() 外接圓的圓心,其中
外接圓的圓心,其中![]() 為直徑,大小為
為直徑,大小為![]() ,
,
故矩形![]() 對角線長為定值
對角線長為定值![]() .
.


科目:高中數(shù)學(xué) 來源: 題型:
【題目】某公司欲生產(chǎn)一款迎春工藝品回饋消費者,工藝品的平面設(shè)計如圖所示,該工藝品由直角![]() 和以
和以![]() 為直徑的半圓拼接而成,點
為直徑的半圓拼接而成,點![]() 為半圈上一點(異于
為半圈上一點(異于![]() ,
,![]() ),點
),點![]() 在線段
在線段![]() 上,且滿足
上,且滿足![]() .已知
.已知![]() ,
,![]() ,設(shè)
,設(shè)![]() .
.

(1)為了使工藝禮品達(dá)到最佳觀賞效果,需滿足![]() ,且
,且![]() 達(dá)到最大.當(dāng)
達(dá)到最大.當(dāng)![]() 為何值時,工藝禮品達(dá)到最佳觀賞效果;
為何值時,工藝禮品達(dá)到最佳觀賞效果;
(2)為了工藝禮品達(dá)到最佳穩(wěn)定性便于收藏,需滿足![]() ,且
,且![]() 達(dá)到最大.當(dāng)
達(dá)到最大.當(dāng)![]() 為何值時,
為何值時,![]() 取得最大值,并求該最大值.
取得最大值,并求該最大值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】下列說法正確的是( )
A. 有兩個平面互相平行,其余各面都是平行四邊形的多面體是棱柱
B. 四棱錐的四個側(cè)面都可以是直角三角形
C. 有兩個平面互相平行,其余各面都是梯形的多面體是棱臺
D. 棱臺的各側(cè)棱延長后不一定交于一點
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,在直角梯形ABCD中,AD∥BC,∠BAD=![]() ,AB=BC=
,AB=BC=![]() AD=a,E是AD的中點,O是AC與BE的交點.將△ABE沿BE折起到如圖2中△A1BE的位置,得到四棱錐A1-BCDE.
AD=a,E是AD的中點,O是AC與BE的交點.將△ABE沿BE折起到如圖2中△A1BE的位置,得到四棱錐A1-BCDE.
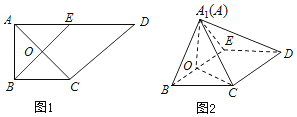
(Ⅰ)證明:CD⊥平面A1OC;
(Ⅱ)當(dāng)平面A1BE⊥平面BCDE時,四棱錐A1-BCDE的體積為36![]() ,求a的值.
,求a的值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】母線長為![]() ,底面半徑為
,底面半徑為![]() 的圓錐內(nèi)有一球
的圓錐內(nèi)有一球![]() ,與圓錐的側(cè)面、底面都相切,現(xiàn)放入一些小球,小球與圓錐底面、側(cè)面、球
,與圓錐的側(cè)面、底面都相切,現(xiàn)放入一些小球,小球與圓錐底面、側(cè)面、球![]() 都相切,這樣的小球最多可放入__________個.
都相切,這樣的小球最多可放入__________個.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
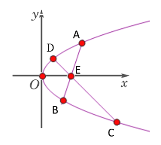
【題目】已知點![]() 為拋物線
為拋物線![]() 內(nèi)一定點,過
內(nèi)一定點,過![]() 作兩條直線交拋物線于
作兩條直線交拋物線于![]() ,且
,且![]() 分別是線段
分別是線段![]() 的中點.
的中點.
(1)當(dāng)![]() 時,求△
時,求△![]() 的面積的最小值;
的面積的最小值;
(2)若![]() 且
且![]() ,證明:直線
,證明:直線![]() 過定點,并求定點坐標(biāo)。
過定點,并求定點坐標(biāo)。
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】“既要金山銀山,又要綠水青山”。某風(fēng)景區(qū)在一個直徑![]() 為
為![]() 米的半圓形花圓中設(shè)計一條觀光線路。打算在半圓弧上任選一點
米的半圓形花圓中設(shè)計一條觀光線路。打算在半圓弧上任選一點![]() (與
(與![]() 不重合),沿
不重合),沿![]() 修一條直線段小路,在路的兩側(cè)(注意是兩側(cè))種植綠化帶;再沿弧
修一條直線段小路,在路的兩側(cè)(注意是兩側(cè))種植綠化帶;再沿弧![]() 修一條弧形小路,在小路的一側(cè)(注意是一側(cè))種植綠化帶,小路與綠化帶的寬度忽略不計。
修一條弧形小路,在小路的一側(cè)(注意是一側(cè))種植綠化帶,小路與綠化帶的寬度忽略不計。

(1)設(shè)![]() (弧度),將綠化帶的總長度表示為
(弧度),將綠化帶的總長度表示為![]() 的函數(shù)
的函數(shù)![]() ;
;
(2)求綠化帶的總長度![]() 的最大值。
的最大值。
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知橢圓![]() 的離心率是
的離心率是![]() ,且橢圓經(jīng)過點
,且橢圓經(jīng)過點![]() .
.
(1)求橢圓![]() 的標(biāo)準(zhǔn)方程;
的標(biāo)準(zhǔn)方程;
(2)若直線![]() :
: ![]() 與圓
與圓![]() 相切:
相切:
(ⅰ)求圓![]() 的標(biāo)準(zhǔn)方程;
的標(biāo)準(zhǔn)方程;
(ⅱ)若直線![]() 過定點
過定點![]() ,與橢圓
,與橢圓![]() 交于不同的兩點
交于不同的兩點![]() ,與圓
,與圓![]() 交于不同的兩點
交于不同的兩點![]() ,求
,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】2015年12月10日,我國科學(xué)家屠呦呦教授由于在發(fā)現(xiàn)青蒿素和治療瘧疾的療法上的貢獻(xiàn)獲得諾貝爾醫(yī)學(xué)獎,以青蒿素類藥物為主的聯(lián)合療法已經(jīng)成為世界衛(wèi)生組織推薦的抗瘧疾標(biāo)準(zhǔn)療法,目前,國內(nèi)青蒿人工種植發(fā)展迅速,調(diào)查表明,人工種植的青蒿的長勢與海撥高度、土壤酸堿度、空氣濕度的指標(biāo)有極強的相關(guān)性,現(xiàn)將這三項的指標(biāo)分別記為![]() ,并對它們進行量化:0表示不合格,1表示臨界合格,2表示合格,再用綜合指標(biāo)
,并對它們進行量化:0表示不合格,1表示臨界合格,2表示合格,再用綜合指標(biāo)![]() 的值評定人工種植的青蒿的長勢等級,若
的值評定人工種植的青蒿的長勢等級,若![]() ,則長勢為一級;若
,則長勢為一級;若![]() ,則長勢為二極;若
,則長勢為二極;若![]() ,則長勢為三級,為了了解目前人工種植的青蒿的長勢情況,研究人員隨機抽取了10塊青蒿人工種植地,得到如下結(jié)果:
,則長勢為三級,為了了解目前人工種植的青蒿的長勢情況,研究人員隨機抽取了10塊青蒿人工種植地,得到如下結(jié)果:
種植地編號 |
|
|
|
|
|
|
|
|
|
|
|
種植地編號 |
|
|
|
|
|
|
|
|
|
|
|
(1)若該地有青蒿人工種植地180個,試估計該地中長勢等級為三級的個數(shù);
(2)從長勢等級為一級的青蒿人工種植地中隨機抽取兩個,求這兩個人工種植地的綜合指標(biāo)![]() 均為4個概率.
均為4個概率.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com