
【題目】.已知函數![]() .
.
(1)求過點![]() 的
的![]() 圖象的切線方程;
圖象的切線方程;
(2)若函數![]() 存在兩個極值點
存在兩個極值點![]() ,
, ![]() ,求
,求![]() 的取值范圍;
的取值范圍;
(3)當![]() 時,均有
時,均有![]() 恒成立,求
恒成立,求![]() 的取值范圍.
的取值范圍.
【答案】(1) ![]() (2)
(2) ![]() (3)
(3) ![]()
【解析】試題分析:(1)設切點坐標為![]() ,則切線方程為
,則切線方程為 ![]() ,根據點
,根據點![]() 坐標,即可求出
坐標,即可求出![]() ,從而得到切線方程;(2)對
,從而得到切線方程;(2)對![]() 求導,令
求導,令![]() ,要使
,要使![]() 存在兩個極值點
存在兩個極值點![]() ,
, ![]() ,則方程
,則方程![]() 有兩個不相等的正數根,從而只需滿足
有兩個不相等的正數根,從而只需滿足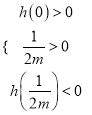 即可;(3)由
即可;(3)由![]() 在
在![]() 上恒成立可得
上恒成立可得![]() 在
在![]() 上恒成立,令
上恒成立,令![]() ,求出
,求出![]() 的單調性,可得出
的單調性,可得出![]() 的最大值,即可求得
的最大值,即可求得![]() 的取值范圍.
的取值范圍.
試題解析:(1)由題意得,函數![]() 的定義域為
的定義域為![]() ,
, ![]()
設切點坐標為![]() ,則切線方程為
,則切線方程為 ![]()
把點![]() 代入切線方程,得:
代入切線方程,得: ![]() ,
,
![]()
![]() 過點
過點![]() 的切線方程為:
的切線方程為: ![]()
(2)∵![]()
∴![]()
令![]()
要使![]() 存在兩個極值點
存在兩個極值點![]() ,
, ![]() ,則方程
,則方程![]() 有兩個不相等的正數根.
有兩個不相等的正數根.
又![]() ,
, ![]() .
.
故只需滿足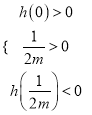 即可
即可
解得: ![]()
(3)由于![]() 在
在![]() 上恒成立.
上恒成立.
∴![]() 在
在![]() 上恒成立.
上恒成立.
令![]()
則![]()
當![]() 時,
時, ![]()
令![]() ,則
,則![]()
![]()
![]() 在
在![]() 上單調遞增
上單調遞增
又![]() ,
, ![]()
∴存在![]() 便得
便得![]() ,即
,即![]() ,
, ![]()
故當![]() 時,
時, ![]() ,此時
,此時![]()
當時![]() ,
, ![]() 此時
此時![]() .
.
故函數![]() 在
在![]() 上遞增,在
上遞增,在![]() 上遞減
上遞減
從而: ![]()
令![]() ,
, ![]()
則![]()
![]()
![]() 在上
在上![]() 單調遞增,
單調遞增,
∴![]()
故![]() .
.


 名校課堂系列答案
名校課堂系列答案科目:高中數學 來源: 題型:
【題目】如圖,在平面直角坐標系xOy中,橢圓C:![]() 的焦點為F1(–1、0),
的焦點為F1(–1、0),
F2(1,0).過F2作x軸的垂線l,在x軸的上方,l與圓F2:![]() 交于點A,與橢圓C交于點D.連結AF1并延長交圓F2于點B,連結BF2交橢圓C于點E,連結DF1.已知DF1=
交于點A,與橢圓C交于點D.連結AF1并延長交圓F2于點B,連結BF2交橢圓C于點E,連結DF1.已知DF1=![]() .
.

(1)求橢圓C的標準方程;
(2)求點E的坐標.
查看答案和解析>>
科目:高中數學 來源: 題型:
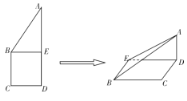
【題目】如圖,正方形![]() 的邊長為
的邊長為![]() ,已知
,已知![]() ,將
,將![]() 沿
沿![]() 邊折起,折起后
邊折起,折起后![]() 點在平面
點在平面![]() 上的射影為
上的射影為![]() 點,則翻折后的幾何體中有如下描述:
點,則翻折后的幾何體中有如下描述:
①![]() 與
與![]() 所成角的正切值是
所成角的正切值是![]() ;
;
②![]() ;
;
③![]() 是
是![]() ;
;
④平面![]() 平面
平面![]() ;
;
⑤直線![]() 與平面
與平面![]() 所成角為30°.
所成角為30°.
其中正確的有________.(填寫你認為正確的序號)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】拋物線的圖象關于![]() 軸對稱,頂點在坐標原點,點
軸對稱,頂點在坐標原點,點![]() 在拋物線上.
在拋物線上.
(1)求拋物線的標準方程;
(2)設直線![]() 的方程為
的方程為![]() ,若直線
,若直線![]() 與拋物線交于
與拋物線交于![]() 兩點,且以
兩點,且以![]() 為直徑的圓過點
為直徑的圓過點![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com