
設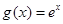 ,
, ,其中
,其中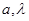 是常數,且
是常數,且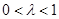 .
.
(1)求函數 的極值;
的極值;
(2)證明:對任意正數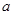 ,存在正數
,存在正數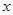 ,使不等式
,使不等式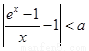 成立;
成立;
(3)設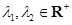 ,且
,且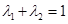 ,證明:對任意正數
,證明:對任意正數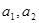 都有:
都有: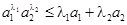 .
.
(1) 當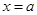 時,
時,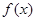 取極大值,但
取極大值,但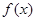 沒有極小值;(2)詳見解析;(3)詳見解析.
沒有極小值;(2)詳見解析;(3)詳見解析.
【解析】
試題分析:(1)先求導,再討論函數的單調區間,然后寫出函數的極值;(2)通過依次構造函數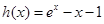 、
、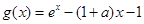 和
和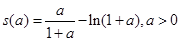 ,利用導數來研究其單調性和最值情況,從而用來比較大小,最終達到證明不等式的目的; (3)先把所要證明的不等式的左邊轉變到函數
,利用導數來研究其單調性和最值情況,從而用來比較大小,最終達到證明不等式的目的; (3)先把所要證明的不等式的左邊轉變到函數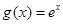 的問題,得到相關的不等式
的問題,得到相關的不等式 ,再借助(1)中
,再借助(1)中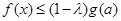 的結論得到
的結論得到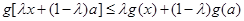 ,最后取
,最后取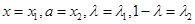 即可證得.
即可證得.
試題解析:(1)∵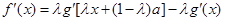 ,
1分
,
1分
由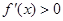 得,
得,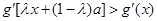 ,
,
∴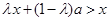 ,即
,即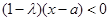 ,解得
,解得 , 3分
, 3分
故當 時,
時,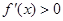 ;當
;當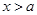 時,
時,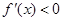 ;
;
∴當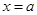 時,
時,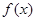 取極大值,但
取極大值,但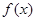 沒有極小值. 4分
沒有極小值. 4分
(2)∵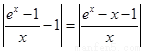 ,又當
,又當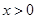 時,令
時,令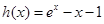 ,則
,則
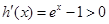 ,
,
故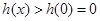 ,因此原不等式化為
,因此原不等式化為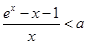 ,即
,即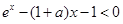 ,
,
令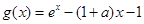 ,則
,則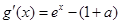 ,
,
由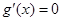 得:
得: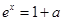 ,解得
,解得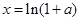 ,
,
當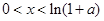 時,
時,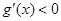 ;當
;當 時,
時,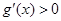 .
.
故當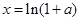 時,
時,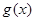 取最小值
取最小值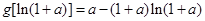 , 8分
, 8分
令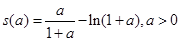 ,則
,則 .
.
故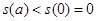 ,即
,即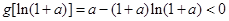 .
.
因此,存在正數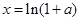 ,使原不等式成立. 10分
,使原不等式成立. 10分
(3)對任意正數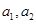 ,存在實數
,存在實數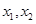 使
使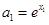 ,
,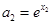 ,
,
則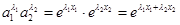 ,
,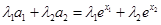 ,
,
原不等式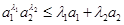
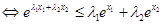 ,
,
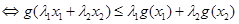 12分
12分
由(1)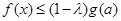 恒成立,故
恒成立,故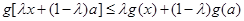 ,
,
取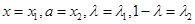 ,即得
,即得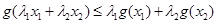 ,
,
即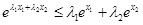 ,故所證不等式成立. 14分
,故所證不等式成立. 14分
考點:1、導數的應用,2、函數單調性的應用,3、不等式的證明.


 名校課堂系列答案
名校課堂系列答案科目:高中數學 來源: 題型:
| π |
| 4 |
| π |
| 4 |
| 1 |
| 2 |
| 3 |
| 5 |
| π |
| 2 |
| 3π |
| 2 |
查看答案和解析>>
科目:高中數學 來源: 題型:
|
| 1 |
| x+1 |
| 1 |
| |P1P2|2 |
| 1 |
| |P1P3|2 |
| 1 |
| |P1Pn|2 |
| 2 |
| 5 |
查看答案和解析>>
科目:高中數學 來源:2007-2008學年北京市西城區高一(上)期末數學試卷(解析版) 題型:解答題
 .先把y=f(x)的圖象上所有點向左平移
.先把y=f(x)的圖象上所有點向左平移 個單位長度,再把所得圖象上所有點的橫坐標縮短到原來的
個單位長度,再把所得圖象上所有點的橫坐標縮短到原來的 (縱坐標不變)得到函數y=g(x)的圖象.
(縱坐標不變)得到函數y=g(x)的圖象.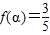 ,
,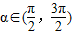 ,求f(2α)的值;
,求f(2α)的值;查看答案和解析>>
科目:高中數學 來源:2011-2012學年山東省高三12月月考理科數學試卷 題型:解答題
某唱片公司要發行一張名為《春風再美也比不上你的笑》的唱片,包含《新花好月圓》、《荷塘月色》等10首創新經典歌曲。該公司計劃用 (百萬元)請李子恒老師進行創作,經調研知:該唱片的總利潤
(百萬元)請李子恒老師進行創作,經調研知:該唱片的總利潤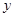 (百萬元)與
(百萬元)與 成正比的關系,當
成正比的關系,當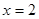 時
時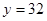 .又有
.又有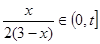 ,其中
,其中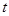 是常數,且
是常數,且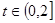 .
.
(Ⅰ)設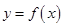 ,求其表達式,定義域(用
,求其表達式,定義域(用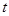 表示);
表示);
(Ⅱ)求總利潤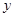 的最大值及相應的
的最大值及相應的 的值.
的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com