【題目】已知橢圓C:
的長軸長為4,離心率為
,點P在橢圓C上.
(1)求橢圓C的標準方程；
(2)已知點M (4,0),點N(0,n),若以PM為直徑的圓恰好經過線段PN的中點,求n的取值范圍.
【答案】(1) 
； (2) 
.
【解析】
（1）根據長軸長和離心率求出標準方程；
（2）取PN的中點為Q，以PM為直徑的圓恰好經過線段PN的中點，所以MQ⊥NP,根據垂直關系建立等量關系，結合點P的坐標取值范圍，即可得解.
解:( 1)由橢圓的長軸長2a=4,得a=2
又離心率
,所以
所以
.
所以橢圓C的方程為：.
(2)法一:設點
,則
所以PN的中點
,
，
因為以PM為直徑的圓恰好經過線段PN的中點
所以MQ⊥NP,則
，
即
，
又因為,所以
，
所以
，
函數
的值域為
所以
所以.
法二:設點,則.
設PN的中點為Q
因為以PM為直徑的圓恰好經過線段PN的中點
所以MQ是線段PN的垂直平分線，
所以
即
所以
，
函數的值域為
所以，
所以.
科目：高中數學 來源： 題型：
【題目】某企業新研發了一種產品，產品的成本由原料成本及非原料成本組成.每件產品的非原料成本
（元）與生產該產品的數量
（千件）有關，經統計得到如下數據：
根據以上數據，繪制了散點圖.
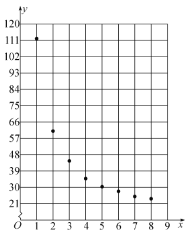
觀察散點圖，兩個變量不具有線性相關關系，現考慮用反比例函數模型
和指數函數模型
分別對兩個變量的關系進行擬合.已求得用指數函數模型擬合的回歸方程為
，
與的相關系數
.參考數據（其中
）：
（1）用反比例函數模型求關于的回歸方程；
（2）用相關系數判斷上述兩個模型哪一個擬合效果更好（精確到0.01），并用其估計產量為10千件時每件產品的非原料成本；
（3）該企業采取訂單生產模式（根據訂單數量進行生產，即產品全部售出）.根據市場調研數據，若該產品單價定為100元，則簽訂9千件訂單的概率為0.8，簽訂10千件訂單的概率為0.2；若單價定為90元，則簽訂10千件訂單的概率為0.3，簽訂11千件訂單的概率為0.7.已知每件產品的原料成本為10元，根據（2）的結果，企業要想獲得更高利潤，產品單價應選擇100元還是90元，請說明理由.
參考公式：對于一組數據
，
，…，
，其回歸直線
的斜率和截距的最小二乘估計分別為：
，
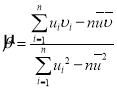，相關系數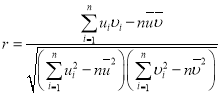
.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，在四棱錐P-ABCD中，底面為正方形，△PAD為等邊三角形，平面PAD丄平面PCD.
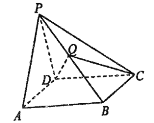
(1)證明：平面PAD丄平面ABCD:
(2)若AB=2，Q為線段的中點，求三棱錐Q-PCD的體積.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數
在區間
上的最大值為
，最小值為
，記
（1）求實數
、
的值；
（2）若不等式
成立，求實數
的取值范圍；
（3）對于任意滿足
的自變量
，
，
，
，
，
，如果存在一個常數
，使得定義在區間
上的一個函數
，有
恒成立，則稱為區間上的有界變差函數，試判斷
是否區間
上的有界變差函數，若是，求出
的最小值；若不是，請說明理由.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖,在六棱錐P﹣ABCDEF中,六邊形ABCDEF為正六邊形,平面PAB⊥平面ABCDEF,AB=1,PA
,PB=2.
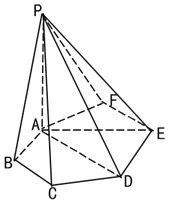
(1)求證:PA⊥平面ABCDEF;
(2)求直線PD與平面PAE所成角的正弦值.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】新中國昂首闊步地走進2019年，迎來了她70歲華誕.某平臺組織了“偉大的復興之路一新中國70周年知識問答”活動，規則如下：共有30道單選題，每題4個選項中只有一個正確，每答對一題獲得5顆紅星，每答錯一題反扣2顆紅星；若放棄此題，則紅星數無變化.答題所獲得的紅星可用來兌換神秘禮品，紅星數越多獎品等級越高.小強參加該活動，其中有些題目會做，有些題目可以排除若干錯誤選項，其余的題目則完全不會.
（1）請問：對于完全不會的題目，小強應該隨機從4個選項中選一個作答，還是選擇放棄？（利用統計知識說明理由）
（2）若小強有12道題目會做，剩下的題目中，可以排除一個錯誤選項、可以排除兩個錯誤選項和完全不會的題目的數量比是
.請問：小強在本次活動中可以獲得最多紅星數的期望是多少？
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
