
【題目】已知![]() 是定義在
是定義在![]() 上的偶函數(shù),滿足
上的偶函數(shù),滿足![]() ,當(dāng)
,當(dāng)![]() 時(shí),
時(shí),![]() ,若
,若![]() ,
,![]() ,
,![]() ,則
,則![]() ,
,![]() ,
,![]() 的大小關(guān)系為( )
的大小關(guān)系為( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】B
【解析】
根據(jù)題意,分析可得函數(shù)f(x)是周期為2的周期函數(shù),據(jù)此可得c=f(2019)=f(1+2×1007)=f(1),b=f(log24.1)=f(log24.1﹣2)=f(log2![]() ),結(jié)合函數(shù)的奇偶性可得a=f(log2
),結(jié)合函數(shù)的奇偶性可得a=f(log2![]() )=f(﹣log2
)=f(﹣log2![]() )=f(log2
)=f(log2![]() ),結(jié)合函數(shù)解析式可得f(x)在[0,1]上為增函數(shù),據(jù)此分析可得答案.
),結(jié)合函數(shù)解析式可得f(x)在[0,1]上為增函數(shù),據(jù)此分析可得答案.
根據(jù)題意,f(x)滿足f(x+2)=f(x),即函數(shù)f(x)是周期為2的周期函數(shù),
則c=f(2019)=f(1+2×1009)=f(1),b=f(log24.1)=f(log24.1﹣2)=f(log2![]() ),
),
又由f(x)為偶函數(shù),則a=f(log2![]() )=f(﹣log2
)=f(﹣log2![]() )=f(log2
)=f(log2![]() ),
),
當(dāng)x∈[0,1]時(shí),f(x)=x3+x,易得f(x)在[0,1]上為增函數(shù),又由0<log2![]() log2
log2![]() 1,
1,
則有b<a<c;
故選:B.



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知拋物線![]() :
:![]() 的焦點(diǎn)為
的焦點(diǎn)為![]() ,直線
,直線![]() 與
與![]() 交于
交于![]() ,
,![]() 兩點(diǎn),且與
兩點(diǎn),且與![]() 軸交于點(diǎn)
軸交于點(diǎn)![]() .
.
(1)若直線![]() 的斜率
的斜率![]() ,且
,且![]() ,求
,求![]() 的值;
的值;
(2)若![]() ,
,![]() 軸上是否存在點(diǎn)
軸上是否存在點(diǎn)![]() ,總有
,總有![]() ?若存在,求出點(diǎn)
?若存在,求出點(diǎn)![]() 坐標(biāo);若不存在,請說明理由.
坐標(biāo);若不存在,請說明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() .
.
(1)當(dāng)![]() 時(shí),求
時(shí),求![]() 在區(qū)間
在區(qū)間![]() 上的最值;
上的最值;
(2)討論函數(shù)![]() 的單調(diào)性;
的單調(diào)性;
(3)當(dāng)![]() 時(shí),有
時(shí),有![]() 恒成立,求
恒成立,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() (
(![]() 為自然對數(shù)的底數(shù)).
為自然對數(shù)的底數(shù)).
(1)求函數(shù)![]() 的極值;
的極值;
(2)問:是否存在實(shí)數(shù)![]() ,使得
,使得![]() 有兩個(gè)相異零點(diǎn)?若存在,求出
有兩個(gè)相異零點(diǎn)?若存在,求出![]() 的取值范圍;若不存在,請說明理由.
的取值范圍;若不存在,請說明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】二十四節(jié)氣是中國古代的一種指導(dǎo)農(nóng)事的補(bǔ)充歷法,是我國勞動(dòng)人民長期經(jīng)驗(yàn)的積累成果和智慧的結(jié)晶,被譽(yù)為“中國的第五大發(fā)明”.由于二十四節(jié)氣對古時(shí)候農(nóng)事的進(jìn)行起著非常重要的指導(dǎo)作用,所以勞動(dòng)人民編寫了很多記憶節(jié)氣的歌謠:春雨驚春清谷天,夏滿芒夏暑相連,秋處露秋寒霜降,冬雪雪冬小大寒.《易經(jīng)》里對二十四節(jié)氣的晷影長的記錄中,冬至和夏至的晷影長是實(shí)測得到的,其他節(jié)氣的晷影是按照等差數(shù)列的規(guī)律計(jì)算出來的,在下表中,冬至的晷影最長為130.0寸,夏至的晷影最短為14.8寸,那么《易經(jīng)》中所記錄的清明的晷影長應(yīng)為( )

A.77.2寸B.72.4寸C.67.3寸D.62.8寸
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知定義域?yàn)?/span>![]() 的奇函數(shù)
的奇函數(shù)![]() ,滿足
,滿足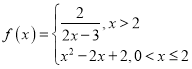 ,下面四個(gè)關(guān)于函數(shù)
,下面四個(gè)關(guān)于函數(shù)![]() 的說法:①存在實(shí)數(shù)
的說法:①存在實(shí)數(shù)![]() ,使關(guān)于
,使關(guān)于![]() 的方程
的方程![]() 有
有![]() 個(gè)不相等的實(shí)數(shù)根;②當(dāng)
個(gè)不相等的實(shí)數(shù)根;②當(dāng)![]() 時(shí),恒有
時(shí),恒有![]() ;③若當(dāng)
;③若當(dāng)![]() 時(shí),
時(shí),![]() 的最小值為
的最小值為![]() ,則
,則![]() ;④若關(guān)于
;④若關(guān)于![]() 的方程
的方程![]() 和
和![]() 的所有實(shí)數(shù)根之和為零,則
的所有實(shí)數(shù)根之和為零,則![]() .其中說法正確的有______.(將所有正確說法的標(biāo)號(hào)填在橫線上)
.其中說法正確的有______.(將所有正確說法的標(biāo)號(hào)填在橫線上)
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() .(其中
.(其中![]() 為自然對數(shù)的底數(shù))
為自然對數(shù)的底數(shù))
(1)若![]() ,且
,且![]() 在
在![]()
![]() 上是增函數(shù),求
上是增函數(shù),求![]() 的最小值;
的最小值;
(2)設(shè)![]() ,若對任意
,若對任意![]() 、
、![]() 恒有
恒有![]() ,求
,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() .
.
(1)求函數(shù)![]() 在點(diǎn)
在點(diǎn)![]() 處的切線方程;
處的切線方程;
(2)求函數(shù)![]() 在
在![]() 上的值域;
上的值域;
(3)若存在![]() ,使得
,使得![]() 成立,求
成立,求![]() 的最大值.(其中自然常數(shù)
的最大值.(其中自然常數(shù)![]() )
)
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com