
【題目】如圖,矩形![]() 所在的半平面和直角梯形
所在的半平面和直角梯形![]() 所在的半平面成
所在的半平面成![]() 的二面角,
的二面角,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
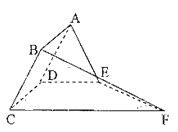
(Ⅰ)求證:平面![]() 平面
平面![]() ;
;
(Ⅱ)試問在線段![]() 上是否存在一點
上是否存在一點![]() ,使銳二面角
,使銳二面角![]() 的余弦值為
的余弦值為![]() .若存在,請求出
.若存在,請求出![]() 的值;若不存在,請說明理由.
的值;若不存在,請說明理由.
【答案】(Ⅰ)見證明;(Ⅱ)見解析
【解析】
(Ⅰ)根據(jù)二面角的平面角的定義得到![]() 即為二面角
即為二面角![]() 的平面角
的平面角![]() ,根據(jù)
,根據(jù)![]() ,
,![]() 得到線面垂直,進而得到面面垂直;(Ⅱ)根據(jù)二面角的平面角的定義,結(jié)合三垂線法做出平面角
得到線面垂直,進而得到面面垂直;(Ⅱ)根據(jù)二面角的平面角的定義,結(jié)合三垂線法做出平面角![]() 是銳二面角
是銳二面角![]() 的平面角,由幾何關(guān)系得到相應結(jié)果即可.
的平面角,由幾何關(guān)系得到相應結(jié)果即可.
(Ⅰ)證明:∵![]() ,
,![]() ,
,
∴![]() 即為二面角
即為二面角![]() 的平面角,
的平面角,
∴![]() .
.
又∵![]() ,
,
∴![]() 平面
平面![]() ,
,
又∵![]() 平面
平面![]() ,
,
∴平面![]() 平面
平面![]() .
.
(Ⅱ)在線段![]() 上存在一點
上存在一點![]() ,當
,當![]() 符合題意,
符合題意,
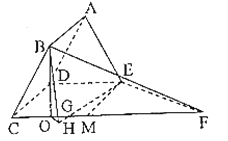
∵平面![]() 平面
平面![]() ,在平面
,在平面![]() 內(nèi),作
內(nèi),作![]() 于
于![]() ,
,
又∵平面![]() 平面
平面![]() ,則
,則![]() 平面
平面![]() .
.
過![]() 作
作![]() 于H,連接
于H,連接![]() ,∵
,∵![]() 為
為![]() 在平面
在平面![]() 的射影,
的射影,
∴![]() 是銳二面角
是銳二面角![]() 的平面角,
的平面角,
因為![]() ,又因為銳二面角
,又因為銳二面角![]() 的余弦值是
的余弦值是![]() ,
,
所以![]() .
.
取![]() 中點
中點![]() ,易知
,易知![]() 與
與![]() 相似,設
相似,設![]() ,則
,則![]() ,
,
即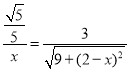 ,解得
,解得![]() 或
或![]() (舍),
(舍),
因此存在符合題意的點![]() ,使得
,使得![]() .
.


科目:高中數(shù)學 來源: 題型:
【題目】某地下車庫在排氣扇發(fā)生故障的情況下,測得空氣中一氧化碳含量達到了危險狀態(tài),經(jīng)搶修,排氣扇恢復正常.排氣![]() 后,測得車庫內(nèi)的一氧化碳濃度為
后,測得車庫內(nèi)的一氧化碳濃度為![]() ,繼續(xù)排氣
,繼續(xù)排氣![]() ,又測得濃度為
,又測得濃度為![]() ,經(jīng)檢測知該地下車庫一氧化碳濃度
,經(jīng)檢測知該地下車庫一氧化碳濃度![]() 與排氣時間
與排氣時間![]() 存在函數(shù)關(guān)系:
存在函數(shù)關(guān)系: (
(![]() ,
,![]() 為常數(shù))。
為常數(shù))。
(1)求![]() ,
,![]() 的值;
的值;
(2)若地下車庫中一氧化碳濃度不高于![]() 為正常,問至少排氣多少分鐘,這個地下車庫中的一氧化碳含量才能達到正常狀態(tài)?
為正常,問至少排氣多少分鐘,這個地下車庫中的一氧化碳含量才能達到正常狀態(tài)?
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】設函數(shù)![]() =Asin
=Asin![]() (A>0,
(A>0,![]() >0,
>0,![]() <
<![]() ≤
≤![]() )在
)在![]() 處取得最大值2,其圖象與x軸的相鄰兩個交點的距離為
處取得最大值2,其圖象與x軸的相鄰兩個交點的距離為![]() 。
。
(1)求![]() 的解析式;
的解析式;
(2)求函數(shù)![]()
![]() 的值域。
的值域。
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知以點![]() 為圓心的圓過原點
為圓心的圓過原點![]() .
.
(1)設直線![]() 與圓
與圓![]() 交于點
交于點![]() ,若
,若![]() ,求圓
,求圓![]() 的方程;
的方程;
(2)在(1)的條件下,設![]() ,且
,且![]() 分別是直線
分別是直線![]() 和圓
和圓![]() 上的動點,求
上的動點,求![]() 的最大值及此時點
的最大值及此時點![]() 的坐標.
的坐標.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】設三棱錐![]() 的底面是正三角形,側(cè)棱長均相等,
的底面是正三角形,側(cè)棱長均相等,![]() 是棱
是棱![]() 上的點(不含端點),記直線
上的點(不含端點),記直線![]() 與直線
與直線![]() 所成角為
所成角為![]() ,直線
,直線![]() 與平面
與平面![]() 所成角為
所成角為![]() ,二面角
,二面角![]() 的平面角為
的平面角為![]() ,則( )
,則( )
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】用6個字母![]() 編擬某種信號程序(大小寫有區(qū)別),把這6個字母全部排列如圖所示的表格中,每個字母必須使用且只使用一次,不同的排列方式表示不同的信號,如果恰有一對字母(同一個字母的大小寫)排到同一列的上下格位置,那么稱此信號為“微錯號”,則不同的“微錯號”的總數(shù)為( )
編擬某種信號程序(大小寫有區(qū)別),把這6個字母全部排列如圖所示的表格中,每個字母必須使用且只使用一次,不同的排列方式表示不同的信號,如果恰有一對字母(同一個字母的大小寫)排到同一列的上下格位置,那么稱此信號為“微錯號”,則不同的“微錯號”的總數(shù)為( )
A.144B.288C.432D.576
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知![]() 是兩個不重合的平面,下列選項中,一定能得出平面
是兩個不重合的平面,下列選項中,一定能得出平面![]() 與平面
與平面![]() 平行的是( )
平行的是( )
A.平面![]() 內(nèi)有一條直線與平面
內(nèi)有一條直線與平面![]() 平行
平行
B.平面![]() 內(nèi)有兩條直線與平面
內(nèi)有兩條直線與平面![]() 平行
平行
C.平面![]() 內(nèi)有一條直線與平面
內(nèi)有一條直線與平面![]() 內(nèi)的一條直線平行
內(nèi)的一條直線平行
D.平面![]() 與平面
與平面![]() 不相交
不相交
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】在數(shù)列![]() 中,若
中,若![]() (
(![]() ,
,![]() ,p為常數(shù)),則
,p為常數(shù)),則![]() 稱為“等方差數(shù)列”.下列對“等方差數(shù)列”的判斷,其中正確的為( )
稱為“等方差數(shù)列”.下列對“等方差數(shù)列”的判斷,其中正確的為( )
A.若![]() 是等方差數(shù)列,則
是等方差數(shù)列,則![]() 是等差數(shù)列
是等差數(shù)列
B.若![]() 是等方差數(shù)列,則
是等方差數(shù)列,則![]() 是等方差數(shù)列
是等方差數(shù)列
C.![]() 是等方差數(shù)列
是等方差數(shù)列
D.若![]() 是等方差數(shù)列,則
是等方差數(shù)列,則![]() (
(![]() ,k為常數(shù))也是等方差數(shù)列
,k為常數(shù))也是等方差數(shù)列
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com