
已知 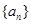 是等差數列,
是等差數列,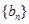 是公比為
是公比為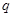 的等比數列,
的等比數列,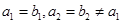 ,記
,記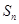 為數列
為數列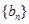 的前
的前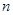 項和,
項和,
(1)若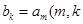 是大于
是大于 的正整數
的正整數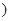 ,求證:
,求證: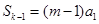 ;
;
(2)若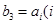 是某一正整數
是某一正整數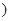 ,求證:
,求證: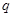 是整數,且數列
是整數,且數列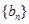 中每一項都是數列
中每一項都是數列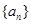 中的項;
中的項;
(3)是否存在這樣的正數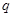 ,使等比數列
,使等比數列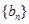 中有三項成等差數列?若存在,寫出一個
中有三項成等差數列?若存在,寫出一個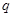 的值,并加以說明;若不存在,請說明理由;
的值,并加以說明;若不存在,請說明理由;
(1)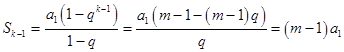
(2)存在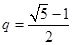 使得
使得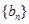 中有三項
中有三項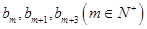 成等差數列。
成等差數列。
解析試題分析:設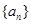 的公差為
的公差為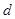 ,由
,由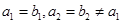 ,知
,知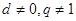 ,
,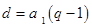 (
(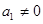 )
)
(1)因為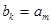 ,所以
,所以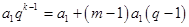 ,
,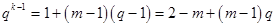 ,
,
所以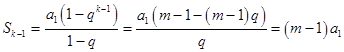
(2)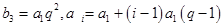 ,由
,由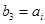 ,
,
所以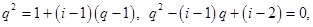 解得,
解得,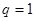 或
或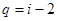 ,但
,但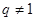 ,所以
,所以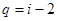 ,因為
,因為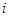 是正整數,所以
是正整數,所以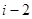 是整數,即
是整數,即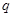 是整數,設數列
是整數,設數列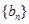 中任意一項為
中任意一項為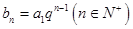 ,設數列
,設數列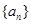 中的某一項
中的某一項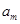
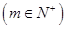 =
=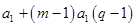
現在只要證明存在正整數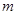 ,使得
,使得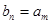 ,即在方程
,即在方程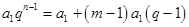 中
中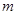 有正整數解即可,
有正整數解即可,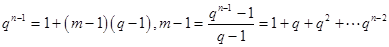 ,所以
,所以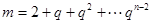 ,若
,若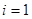 ,則
,則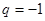 ,那么
,那么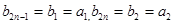 ,當
,當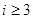 時,因為
時,因為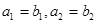 ,只要考慮
,只要考慮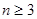 的情況,因為
的情況,因為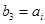 ,所以
,所以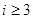 ,因此
,因此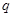 是正整數,所以
是正整數,所以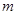 是正整數,因此數列
是正整數,因此數列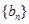 中任意一項為
中任意一項為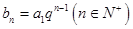 與數列
與數列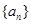 的第
的第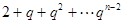 項相等,從而結論成立。
項相等,從而結論成立。
(3)設數列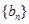 中有三項
中有三項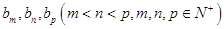 成等差數列,則有
成等差數列,則有
2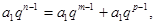 設
設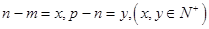 ,所以2
,所以2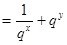 ,令
,令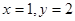 ,則
,則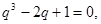
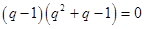 ,因為
,因為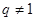 ,所以
,所以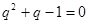 ,所以
,所以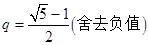 ,即存在
,即存在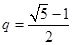 使得
使得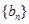 中有三項
中有三項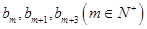 成等差數列。
成等差數列。
考點:本題主要考查等比數列的通項公式、求和公式,等差數列的概念。
點評:難題,等比數列、等差數列相關內容,已是高考必考內容,其難度飄忽不定,有時突出考查求和問題,如“分組求和法”、“裂項相消法”、“錯位相減法”等,有時則突出涉及數列的證明題,如本題,突出考查學生的邏輯思維能力。本題解法中,注意通過構造“一般項”加以研究,帶有普遍性。


科目:高中數學 來源: 題型:解答題
某公司經銷一種數碼產品,第一年可獲利200萬元,從第二年起,由于市場競爭等方面的原因,其利潤每年比上一年減少20萬元,按照這一規律,如果公司不開發新產品,也不調整經營策略,從哪一年起,該公司經銷這一產品將虧損?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com