
【題目】某花卉企業引進了數百種不同品種的康乃馨,通過試驗田培育,得到了這些康乃馨種子在當地環境下的發芽率,并按發芽率分為![]() 組:
組:![]() 、
、![]() 、
、![]() 、
、![]() 加以統計,得到如圖所示的頻率分布直方圖.企業對康乃馨的種子進行分級,將發芽率不低于
加以統計,得到如圖所示的頻率分布直方圖.企業對康乃馨的種子進行分級,將發芽率不低于![]() 的種子定為“
的種子定為“![]() 級”,發芽率低于
級”,發芽率低于![]() 但不低于
但不低于![]() 的種子定為“
的種子定為“![]() 級”,發芽率低于
級”,發芽率低于![]() 的種子定為“
的種子定為“![]() 級”.
級”.
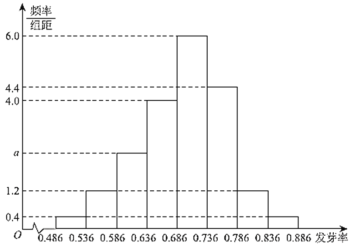
(Ⅰ)現從這些康乃馨種子中隨機抽取一種,估計該種子不是“![]() 級”種子的概率;
級”種子的概率;
(Ⅱ)該花卉企業銷售花種,且每份“![]() 級”、“
級”、“![]() 級”、“
級”、“![]() 級”康乃馨種子的售價分別為
級”康乃馨種子的售價分別為![]() 元、
元、![]() 元、
元、![]() 元.某人在市場上隨機購買了該企業銷售的康乃馨種子兩份,共花費
元.某人在市場上隨機購買了該企業銷售的康乃馨種子兩份,共花費![]() 元,以頻率為概率,求
元,以頻率為概率,求![]() 的分布列和數學期望;
的分布列和數學期望;
(Ⅲ)企業改進了花卉培育技術,使得每種康乃馨種子的發芽率提高到原來的![]() 倍,那么對于這些康乃馨的種子,與舊的發芽率數據的方差相比,技術改進后發芽率數據的方差是否發生變化?若發生變化,是變大了還是變小了?(結論不需要證明).
倍,那么對于這些康乃馨的種子,與舊的發芽率數據的方差相比,技術改進后發芽率數據的方差是否發生變化?若發生變化,是變大了還是變小了?(結論不需要證明).
【答案】(Ⅰ)![]() ;(Ⅱ)分布列詳見解析,數學期望為
;(Ⅱ)分布列詳見解析,數學期望為![]() ;(Ⅲ)方差變大了.
;(Ⅲ)方差變大了.
【解析】
(Ⅰ)利用頻率分布直方圖中矩形面積之和為![]() ,求出
,求出![]() 的值,再結合頻率分布直方圖以及對立事件的概率公式可求得所求事件的概率;
的值,再結合頻率分布直方圖以及對立事件的概率公式可求得所求事件的概率;
(Ⅱ)由題意可知,隨機變量![]() 的可能取值有
的可能取值有![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() ,計算出隨機變量
,計算出隨機變量![]() 在不同取值下的概率,由此可列出隨機變量
在不同取值下的概率,由此可列出隨機變量![]() 的分布列,進而可求得隨機變量
的分布列,進而可求得隨機變量![]() 的數學期望;
的數學期望;
(Ⅲ)根據離散型隨機變量方差的性質可得出結論.
(Ⅰ)設事件![]() 為:“從這些康乃馨種子中隨機抽取一種,且該種子不是“
為:“從這些康乃馨種子中隨機抽取一種,且該種子不是“![]() 級”種子”,
級”種子”,
由圖表,得![]() ,解得
,解得![]() ,
,
由圖表,知“![]() 級”種子的頻率為
級”種子的頻率為![]() ,
,
故可估計從這些康乃馨種子中隨機抽取一種,該種子是“![]() 級”的概率為
級”的概率為![]() .
.
因為事件![]() 與事件“從這些康乃馨種子中隨機抽取一種,且該種子是“
與事件“從這些康乃馨種子中隨機抽取一種,且該種子是“![]() 級”種子”為對立事件,
級”種子”為對立事件,
所以事件![]() 的概率
的概率![]() ;
;
(Ⅱ)由題意,任取一顆種子,恰好是“![]() 級”康乃馨的概率為
級”康乃馨的概率為![]() ,
,
恰好是“![]() 級”康乃馨的概率為
級”康乃馨的概率為![]() ,
,
恰好是“![]() 級”的概率為
級”的概率為![]() .
.
隨機變量![]() 的可能取值有
的可能取值有![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() ,
,
且![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]() .
.
所以![]() 的分布列為:
的分布列為:
|
|
|
|
|
|
|
|
|
|
|
|
故![]() 的數學期望
的數學期望![]() .
.
(Ⅲ)與舊的發芽率數據的方差相比,技術改進后發芽率數據的方差變大了.


科目:高中數學 來源: 題型:
【題目】選修4-4:坐標系與參數方程
在極坐標系中,曲線的極坐標方程為![]() ,以極點為原點,極軸為
,以極點為原點,極軸為![]() 軸的非負半軸建立平面直角坐標系,直線
軸的非負半軸建立平面直角坐標系,直線![]() 的參數方程為
的參數方程為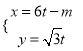 (
(![]() 為參數,
為參數, ![]() ).
).
(1)求曲線![]() 的直角坐標方程和直線
的直角坐標方程和直線![]() 的普通方程;
的普通方程;
(2)若曲線![]() 上的動點
上的動點![]() 到直線
到直線![]() 的最大距離為
的最大距離為![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖是某地某月1日至15日的日平均溫度變化的折線圖,根據該折線圖,下列結論正確的是( )
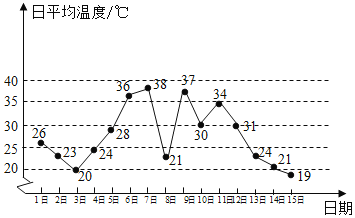
A. 這15天日平均溫度的極差為![]()
B. 連續三天日平均溫度的方差最大的是7日,8日,9日三天
C. 由折線圖能預測16日溫度要低于![]()
D. 由折線圖能預測本月溫度小于![]() 的天數少于溫度大于
的天數少于溫度大于![]() 的天數
的天數
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某部影片的盈利額(即影片的票房收入與固定成本之差)記為![]() ,觀影人數記為
,觀影人數記為![]() ,其函數圖象如圖(1)所示.由于目前該片盈利未達到預期,相關人員提出了兩種調整方案,圖(2)、圖(3)中的實線分別為調整后
,其函數圖象如圖(1)所示.由于目前該片盈利未達到預期,相關人員提出了兩種調整方案,圖(2)、圖(3)中的實線分別為調整后![]() 與
與![]() 的函數圖象.
的函數圖象.

給出下列四種說法:
①圖(2)對應的方案是:提高票價,并提高成本;
②圖(2)對應的方案是:保持票價不變,并降低成本;
③圖(3)對應的方案是:提高票價,并保持成本不變;
④圖(3)對應的方案是:提高票價,并降低成本.
其中,正確的說法是____________.(填寫所有正確說法的編號)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖1,在四邊形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() .把
.把![]() 沿著
沿著![]() 翻折至
翻折至![]() 的位置,
的位置,![]() 平面
平面![]() ,連結
,連結![]() ,如圖2.
,如圖2.
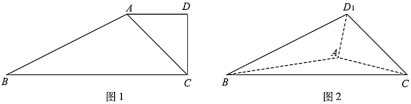
(1)當![]() 時,證明:平面
時,證明:平面![]() 平面
平面![]() ;
;
(2)當三棱錐![]() 的體積最大時,求點
的體積最大時,求點![]() 到平面
到平面![]() 的距離.
的距離.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知![]() 為坐標原點,橢圓
為坐標原點,橢圓![]() 的右焦點為
的右焦點為![]() ,過
,過![]() 的直線
的直線![]() 與
與![]() 相交于
相交于![]() 兩點,點
兩點,點![]() 滿足
滿足![]() .
.
(1)當![]() 的傾斜角為
的傾斜角為![]() 時,求直線
時,求直線![]() 的方程;
的方程;
(2)試探究在![]() 軸上是否存在定點
軸上是否存在定點![]() ,使得
,使得![]() 為定值?若存在,求出點
為定值?若存在,求出點![]() 的坐標;若不存在,請說明理由.
的坐標;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某同學使用某品牌暖水瓶,其內膽規格如圖所示.若水瓶內膽壁厚不計,且內膽如圖分為①②③④四個部分,它們分別為一個半球、一個大圓柱、一個圓臺和一個小圓柱體.若其中圓臺部分的體積為![]() ,且水瓶灌滿水后蓋上瓶塞時水溢出
,且水瓶灌滿水后蓋上瓶塞時水溢出![]() .記蓋上瓶塞后,水瓶的最大盛水量為
.記蓋上瓶塞后,水瓶的最大盛水量為![]() ,
,
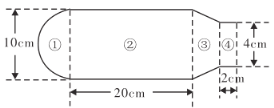
(1)求![]() ;
;
(2)該同學發現:該品牌暖水瓶盛不同體積的熱水時,保溫效果不同.為了研究保溫效果最好時暖水瓶的盛水體積,做以下實驗:把盛有最大盛水量![]() 的水的暖水瓶倒出不同體積的水,并記錄水瓶內不同體積水在不同時刻的水溫,發現水溫
的水的暖水瓶倒出不同體積的水,并記錄水瓶內不同體積水在不同時刻的水溫,發現水溫![]() (單位:℃)與時刻
(單位:℃)與時刻![]() 滿足線性回歸方程
滿足線性回歸方程![]() ,通過計算得到下表:
,通過計算得到下表:
倒出體積 | 0 | 30 | 60 | 90 | 120 |
擬合結果 |
|
|
|
|
|
倒出體積 | 150 | 180 | 210 | … | 450 |
擬合結果 |
|
|
| … |
|
注:表中倒出體積![]() (單位:
(單位:![]() )是指從最大盛水量中倒出的那部分水的體積.其中:
)是指從最大盛水量中倒出的那部分水的體積.其中:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
令![]() .對于數據
.對于數據![]() ,可求得回歸直線為
,可求得回歸直線為![]() ,對于數據
,對于數據![]() ,可求得回歸直線為
,可求得回歸直線為![]() .
.
(ⅰ)指出![]() 的實際意義,并求出回歸直線
的實際意義,并求出回歸直線![]() 的方程(參考數據:
的方程(參考數據:![]() );
);
(ⅱ)若![]() 與
與![]() 的交點橫坐標即為最佳倒出體積,請問保溫瓶約盛多少體積水時(盛水體積保留整數,且
的交點橫坐標即為最佳倒出體積,請問保溫瓶約盛多少體積水時(盛水體積保留整數,且![]() 取3.14)保溫效果最佳?
取3.14)保溫效果最佳?
附:對于一組數據![]() ,其回歸直線
,其回歸直線![]() 中的斜率和截距的最小二乘估計分別為
中的斜率和截距的最小二乘估計分別為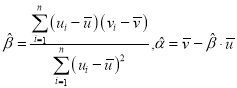 .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com