
【題目】分別求出適合下列條件的直線方程: (Ⅰ)經過點P(﹣3,2)且在x軸上的截距等于在y軸上截距的2倍;
(Ⅱ)經過直線2x+7y﹣4=0與7x﹣21y﹣1=0的交點,且和A(﹣3,1),B(5,7)等距離.
【答案】解:(Ⅰ)當直線不過原點時,設所求直線方程為 ![]() +
+ ![]() =1,
=1,
將(﹣3,2)代入所設方程,解得a= ![]() ,此時,直線方程為x+2y﹣1=0.
,此時,直線方程為x+2y﹣1=0.
當直線過原點時,斜率k=﹣ ![]() ,直線方程為y=﹣
,直線方程為y=﹣ ![]() x,即2x+3y=0,
x,即2x+3y=0,
綜上可知,所求直線方程為x+2y﹣1=0或2x+3y=0.
(Ⅱ)有 ![]() 解得交點坐標為(1,
解得交點坐標為(1, ![]() ),
),
當直線l的斜率k存在時,設l的方程是y﹣ ![]() =k(x﹣1),即7kx﹣7y+(2﹣7k)=0,
=k(x﹣1),即7kx﹣7y+(2﹣7k)=0,
由A、B兩點到直線l的距離相等得 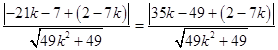 ,
,
解得k= ![]() ,當斜率k不存在時,即直線平行于y軸,方程為x=1時也滿足條件.
,當斜率k不存在時,即直線平行于y軸,方程為x=1時也滿足條件.
所以直線l的方程是21x﹣28y﹣13=0或x=1
【解析】(Ⅰ)分別討論直線過原點和不過原點兩種情況,設出直線方程,解出即可;(Ⅱ)先求出直線的交點坐標,設出直線方程,再根據點到直線的距離公式求出斜率k即可.
【考點精析】利用一般式方程對題目進行判斷即可得到答案,需要熟知直線的一般式方程:關于![]() 的二元一次方程
的二元一次方程![]() (A,B不同時為0).
(A,B不同時為0).


 鴻圖圖書寒假作業假期作業吉林大學出版社系列答案
鴻圖圖書寒假作業假期作業吉林大學出版社系列答案科目:高中數學 來源: 題型:
【題目】下列命題中正確的有 .
①常數數列既是等差數列也是等比數列;
②在△ABC中,若sin2A+sin2B=sin2C,則△ABC為直角三角形;
③若A,B為銳角三角形的兩個內角,則tanAtanB>1;
④若Sn為數列{an}的前n項和,則此數列的通項an=Sn﹣Sn﹣1(n>1).
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在四棱錐P﹣ABCD中,底面ABCD是正方形,側棱PD⊥底面ABCD,PD=DC,E是PC的中點,過E點做EF⊥PB交PB于點F.求證: 
(1)PA∥平面DEB;
(2)PB⊥平面DEF.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2016年9月,第22屆魯臺經貿洽談會在濰坊魯臺會展中心舉行,在會展期間某展銷商銷售一種商品,根據市場調查,每件商品售價x(元)與銷量t(萬元)之間的函數關系如圖所示,又知供貨價格與銷量呈反比,比例系數為20.(注:每件產品利潤=售價﹣供貨價格) 
(1)求售價15元時的銷量及此時的供貨價格;
(2)當銷售價格為多少時總利潤最大,并求出最大利潤.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,等邊三角形OAB的邊長為8 ![]() ,且三個頂點均在拋物線E:y2=2px(p>0)上,O為坐標原點.
,且三個頂點均在拋物線E:y2=2px(p>0)上,O為坐標原點. 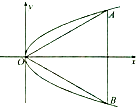
(1)證明:A、B兩點關于x軸對稱;
(2)求拋物線E的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知三棱柱ABC﹣A1B1C1的側棱與底面垂直,體積為 ![]() ,底面是邊長為
,底面是邊長為 ![]() 的正三角形,若P為底面A1B1C1的中心,則PA與平面A1B1C1所成角的大小為( )
的正三角形,若P為底面A1B1C1的中心,則PA與平面A1B1C1所成角的大小為( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】四邊形ABCD是正方形,△PAB與△PAD均是以A為直角頂點的等腰直角三角形,點F是PB的中點,點E是邊BC上的任意一點. 
(1)求證:AF⊥EF;
(2)求二面角A﹣PC﹣B的平面角.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com