【題目】設函數
是定義域為R的奇函數.
（1）求實數k的值；
（2）若
，試判斷函數
的單調性，并求不等式
的解集；
（3）若
，設
，
在
上的最小值為-1，求實數m的值.
【答案】（1）
（2）
為R上的增函數. 
.（3）
【解析】
（1）根據函數
是定義域為R的奇函數，得
，求得
，再驗證可得值；
（2）由
，解得
的范圍，再根據單調性的定義可證得函數的單調性，根據函數的奇偶性可將不等式變形為
，再由函數的單調性可解得不等式的解集；
（3）由
可求得
，從而得出
，再由函數的值域，討論二次函數
的對稱軸與區間的關系得出最小值，可求得參數的值.
（1）因為函數是定義域為R的奇函數，所以，即
，得.
當時，
，
，符合題意.
所以.
（2）由（1）知，，解得
設
，
是任意兩個實數，且
，
則
因為，，
，所以
，
所以
，即
，所以為R上的增函數.
因為是定義域為R的奇函數，所以
，
不等式
同解于.
因為為R上的增函數，所以
，即
，解得
或
，
所以不等式的解集為.
（3）由得
，解得.所以
，
由（2）知是單調遞增函數，因為
，所以
.
令
，則，
.
當
時，函數
在
單調遞增，
不合題意；
當
時，函數在單調遞減，
，解得
；
當
時，函數在
上單調遞減，在
上單調遞增，
，得
（舍去），
綜上可得，實數m的值為.
科目：高中數學 來源： 題型：
【題目】如圖為某市國慶節7天假期的樓房認購量與成交量的折線圖，小明同學根據折線圖對這7天的認購量(單位：套)與成交量(單位：套)作出如下判斷：①日成交量的中位數是16；②日成交量超過日平均成交量的有2天；③認購量與日期正相關；④10月7日認購量的增幅大于10月7日成交量的增幅．則上述判斷正確的個數為( )
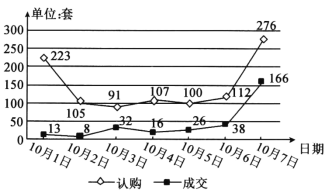
A.0B.1C.2D.3
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知橢圓E：
＋
＝1(a>b>0)的離心率為
，焦點到相應準線的距離為
.
(1) 求橢圓E的標準方程；
(2) 已知P(t，0)為橢圓E外一動點，過點P分別作直線l1和l2，直線l1和l2分別交橢圓E于點A，B和點C，D，且l1和l2的斜率分別為定值k1和k2，求證：
為定值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】給定平面上的五個點
、
、
、
、
，任意三點不共線.由這些點連成4條線段，每個點至少是一條線段的端點.則不同的連結方式有（ ）.
A. 120種 B. 125種 C. 130種 D. 135種
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】學習雷鋒精神前半年內某單位餐廳的固定餐椅經常有損壞，學習雷鋒精神時全修好；單位對學習雷鋒精神前后各半年內餐椅的損壞情況作了一個大致統計，具體數據如下：
損壞餐椅數 | 未損壞餐椅數 | 總 計 | |
學習雷鋒精神前 | 50 | 150 | 200 |
學習雷鋒精神后 | 30 | 170 | 200 |
總 計 | 80 | 320 | 400 |
(1)求:學習雷鋒精神前后餐椅損壞的百分比分別是多少?并初步判斷損毀餐椅數量與學習雷鋒精神是否有關？
(2)請說明是否有97.5%以上的把握認為損毀餐椅數量與學習雷鋒精神有關？
參考公式：
，
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數f(x)＝4cos ωx·sin
＋a(ω>0)圖象上最高點的縱坐標為2，且圖象上相鄰兩個最高點的距離為π.
(1)求a和ω的值；
(2)求函數f(x)在[0，π]上的單調遞減區間.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，在平面直角坐標系
中，點
，直線
，設圓
的半徑為1， 圓心在
上.
（1）若圓心也在直線
上，過點
作圓的切線，求切線方程；
（2）若圓上存在點
，使
，求圓心的橫坐標
的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
