【題目】如圖為某市國慶節7天假期的樓房認購量與成交量的折線圖，小明同學根據折線圖對這7天的認購量(單位：套)與成交量(單位：套)作出如下判斷：①日成交量的中位數是16；②日成交量超過日平均成交量的有2天；③認購量與日期正相關；④10月7日認購量的增幅大于10月7日成交量的增幅．則上述判斷正確的個數為( )
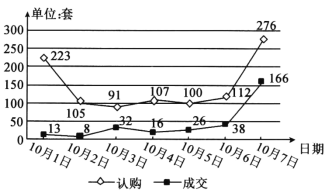
A.0B.1C.2D.3
天天向上口算本系列答案科目：高中數學 來源： 題型：
【題目】每年五月最受七中學子期待的學生活動莫過于學生節，在每屆學生節活動中，著七中校服的布偶“七中熊”尤其受同學和老師歡迎.已知學生會將在學生節當天售賣“七中熊”，并且會將所獲得利潤全部捐獻于公益組織.為了讓更多同學知曉，學生會宣傳部需要前期在學校張貼海報宣傳，成本為250元，并且當學生會向廠家訂制
只“七中熊”時，需另投入成本
，
（元），
.通過市場分析， 學生會訂制的“七中熊”能全部售完.若學生節當天，每只“七中熊”售價為70元，則當銷量為______只時，學生會向公益組織所捐獻的金額會最大.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在數列{an}中，若an2﹣an﹣12＝p，（n≥2，n∈N*，p為常數），則稱{an}為“等方差數列”，下列是對“等方差數列“的判斷：
①若{an}是等方差數列，則{an2}是等差數列；
②{（﹣1）n}是等方差數列；
③若{an}是等方差數列，則{akn}（k∈N*，k為常數）也是等方差數列；
④若{an}既是等方差數列，又是等差數列，則該數列為常數列．
其中正確命題的個數是（ ）
A.1B.2C.3D.4
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知遞增數列{an}前n項和為Sn，且滿足a1＝3，4Sn﹣4n+1＝an2，設bn
（n∈N*)且數列{bn}的前n項和為Tn
（Ⅰ)求證：數列{an}為等差數列；
（Ⅱ)若對任意的n∈N*，不等式λTn
n
（﹣1)n+1恒成立，求實數λ的取值范圍．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】為了適應高考改革，某中學推行“創新課堂”教學．高一平行甲班采用“傳統教學”的教學方式授課，高一平行乙班采用“創新課堂”的教學方式授課，為了比較教學效果，期中考試后，分別從兩個班中各隨機抽取
名學生的成績進行統計分析，結果如下表：（記成績不低于
分者為“成績優秀”）
分數 |
|
|
|
|
|
|
|
甲班頻數 |
|
|
|
|
|
|
|
乙班頻數 |
|
|
|
|
|
|
|
（Ⅰ）由以上統計數據填寫下面的
列聯表，并判斷是否有
以上的把握認為“成績優秀與教學方式有關”？
甲班 | 乙班 | 總計 | |
成績優秀 | |||
成績不優秀 | |||
總計 |
（Ⅱ）現從上述樣本“成績不優秀”的學生中，抽取
人進行考核，記“成績不優秀”的乙班人數為
，求的分布列和期望．
參考公式：
，其中
．
臨界值表
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某銀行推出一款短期理財產品，約定如下：
（1）購買金額固定；
（2）購買天數可自由選擇，但最短3天，最長不超過10天；
（3）購買天數
與利息
的關系，可選擇下述三種方案中的一種：
方案一：
；方案二：
；方案三：
.
請你根據以上材料，研究下面兩個問題：
（1）結合所學的數學知識和方法，用其它方式刻畫上述三種方案的函數特征；
（2）依據你的分析，給出一個最佳理財方案.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某單位響應黨中央“精準扶貧”號召，對某村6戶貧困戶中的甲戶進行定點幫扶，每年跟蹤調查統計一次，從2015年1月1日至2018年12月底統計數據如下（人均年純收入）：
年份 | 2015年 | 2016年 | 2017年 | 2018年 |
年份代碼 | 1 | 2 | 3 | 4 |
收入 | 25 | 28 | 32 | 35 |
（1）請根據上表提供的數據，用最小二乘法求出
關于
的線性回歸方程
，并估計甲戶在2019年能否脫貧；（國家規定2019年脫貧標準：人均年純收入為3747元）
（2）2019年初，根據扶貧辦的統計知，該村剩余5戶貧困戶中還有2戶沒有脫貧，現從這5戶中抽取2戶，求至少有一戶沒有脫貧的概率．
參考公式：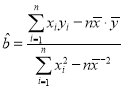
，
，其中
，
為數，的平均數．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知下列各命題：
①兩兩相交且不共點的三條直線確定一個平面：
②若真線
不平行于平面，則直線與平面有公共點：
③若兩個平面垂直，則一個平面內的已知直線必垂直于另一個平面的無數條直線：
④若兩個二面角的兩個面分別對應垂直，則這兩個二面角相等或互補.
則其中正確的命題共有（ ）個
A.
B.
C.
D.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】設函數
是定義域為R的奇函數.
（1）求實數k的值；
（2）若
，試判斷函數
的單調性，并求不等式
的解集；
（3）若
，設
，
在
上的最小值為-1，求實數m的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
