
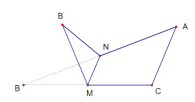
【題目】如圖,∠C=![]() ,
,![]() ,M,N分別是BC,AB的中點,將△BMN沿直線MN折起,使二面角B'-MN-B的大小為
,M,N分別是BC,AB的中點,將△BMN沿直線MN折起,使二面角B'-MN-B的大小為![]() ,則B'N與平面ABC所成角的正切值是( )
,則B'N與平面ABC所成角的正切值是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】C
【解析】
由∠C=![]() ,
,![]() ,先得到∠B′ND就為斜線B′N與平面ABC所成的角設為α,設BC=2,AC=
,先得到∠B′ND就為斜線B′N與平面ABC所成的角設為α,設BC=2,AC=![]() ,BM=B'M=1,DM=B'Mcos60°=
,BM=B'M=1,DM=B'Mcos60°=![]() ,B'D=B'Msin60°=
,B'D=B'Msin60°=![]() ,又MN=
,又MN=![]() ,所以DN=
,所以DN=![]() ,所以tanα=
,所以tanα=![]() ,解出即可.
,解出即可.
解:∵∠C=![]() ,
,![]() ,M、N分別是BC、AB的中點,
,M、N分別是BC、AB的中點,
將△BMN沿直線MN折起,使二面角B′-MN-B的大小為![]() .∴∠BMB′=
.∴∠BMB′=![]() ,
,
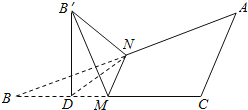
取BM的中點D,連B′D,ND,
由于折疊之前BM與CM都始終垂直于MN,這在折疊之后仍然成立,
∴折疊之后平面B′MN與平面BMN所成的二面角即為∠B′MD=60°,
并且B′在底面ACB內的投影點D就在BC上,∴B′D⊥BC,B′D⊥AD,B′D⊥面ABC,
∴∠B′ND就為斜線B′N與平面ABC所成的角設為α,
設BC=2,AC=![]() ,BM=B'M=1,DM=B'Mcos60°=
,BM=B'M=1,DM=B'Mcos60°=![]() ,B'D=B'Msin60°=
,B'D=B'Msin60°=![]() ,
,
又MN=![]() ,所以DN=
,所以DN=![]() ,
,
所以tanα=![]() =
=![]() =
=![]() .
.
故選C.


 同步輕松練習系列答案
同步輕松練習系列答案 課課通課程標準思維方法與能力訓練系列答案
課課通課程標準思維方法與能力訓練系列答案科目:高中數學 來源: 題型:
【題目】命題![]() :方程
:方程![]() 表示焦點在
表示焦點在![]() 軸上的雙曲線:命題
軸上的雙曲線:命題![]() :若存在
:若存在![]() ,使得
,使得![]() 成立.
成立.
(1)如果命題![]() 是真命題,求實數
是真命題,求實數![]() 的取值范圍;
的取值范圍;
(2)如果“![]() ”為假命題,“
”為假命題,“![]() ”為真命題,求實數
”為真命題,求實數![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為響應綠色出行,某市在推出“共享單車”后,又推出“新能源租賃汽車”.每次租車收費的標準由兩部分組成:①里程計費:1元/公里;②時間計費:![]() 元/分.已知陳先生的家離上班公司
元/分.已知陳先生的家離上班公司![]() 公里,每天上、下班租用該款汽車各一次.一次路上開車所用的時間記為
公里,每天上、下班租用該款汽車各一次.一次路上開車所用的時間記為![]() (分),現統計了50次路上開車所用時間,在各時間段內頻數分布情況如下表所示
(分),現統計了50次路上開車所用時間,在各時間段內頻數分布情況如下表所示

將各時間段發生的頻率視為概率,一次路上開車所用的時間視為用車時間,范圍為![]()
![]() 分.
分.
(1)估計陳先生一次租用新能源租賃汽車所用的時間不低于![]() 分鐘的概率;
分鐘的概率;
(2)若公司每月發放![]() 元的交通補助費用,請估計是否足夠讓陳先生一個月上下班租用新能源租賃汽車(每月按
元的交通補助費用,請估計是否足夠讓陳先生一個月上下班租用新能源租賃汽車(每月按![]() 天計算),并說明理由.(同一時段,用該區間的中點值作代表)
天計算),并說明理由.(同一時段,用該區間的中點值作代表)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() ,四點
,四點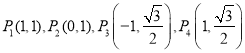 中恰有三點在橢圓上.
中恰有三點在橢圓上.
(1)求橢圓C的方程
(2)橢圓C上是否存在不同的兩點M,N關于直線![]() 對稱?若存在,請求出直線MN的方程,若不存在,請說明理由.
對稱?若存在,請求出直線MN的方程,若不存在,請說明理由.
(3)設直線l不經過點![]() 且與C相交于A,B兩點,若直線
且與C相交于A,B兩點,若直線![]() 與直線
與直線![]() 的斜率之和為1,求證直線l必過定點,并求出這個定點坐標.
的斜率之和為1,求證直線l必過定點,并求出這個定點坐標.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖所示,曲線C由部分橢圓C1:![]() +
+![]() =1(a>b>0,y≥0)和部分拋物線C2:y=-x2+1(y≤0)連接而成,C1與C2的公共點為A,B,其中C1所在橢圓的離心率為
=1(a>b>0,y≥0)和部分拋物線C2:y=-x2+1(y≤0)連接而成,C1與C2的公共點為A,B,其中C1所在橢圓的離心率為![]() .
.

(1)求a,b的值;
(2)過點B的直線l與C1,C2分別交于點P,Q(P,Q,A,B中任意兩點均不重合),若AP⊥AQ,求直線l
的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知項數為![]() 項的有窮數列
項的有窮數列![]() ,若同時滿足以下三個條件:
,若同時滿足以下三個條件:
![]() ,
,![]() 為正整數
為正整數![]() ;
;![]() 或1,其中
或1,其中![]() ,3,
,3,![]() ,
,![]() ;
;
![]() 任取數列
任取數列![]() 中的兩項
中的兩項![]() ,
,![]() ,剩下的
,剩下的![]() 項中一定存在兩項
項中一定存在兩項![]() ,
,![]() ,滿足
,滿足![]() ,則稱數列
,則稱數列![]() 為
為![]() 數列.
數列.
![]() 若數列
若數列![]() 是首項為1,公差為1,項數為6項的等差數列,判斷數列
是首項為1,公差為1,項數為6項的等差數列,判斷數列![]() 是否是
是否是![]() 數列,并說明理由.
數列,并說明理由.
![]() 當
當![]() 時,設
時,設![]() 數列
數列![]() 中1出現
中1出現![]() 次,2出現
次,2出現![]() 次,3出現
次,3出現![]() 次,其中
次,其中![]() ,
,![]() ,
,![]() .
.
求證:![]() ,
,![]() ,
,![]() ;
;
![]() 當
當![]() 時,求
時,求![]() 數列
數列![]() 中項數
中項數![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在直角坐標系xOy中,圓C的參數方程為:![]() 為參數
為參數![]() ,以坐標原點為極點,x軸的非負半軸為極軸建立極坐標系,射線l的極坐標方程為
,以坐標原點為極點,x軸的非負半軸為極軸建立極坐標系,射線l的極坐標方程為![]() ,
,![]() .
.
![]() 將圓C的參數方程化為極坐標方程;
將圓C的參數方程化為極坐標方程;
![]() 設點A的直角坐標為
設點A的直角坐標為![]() ,射線l與圓C交于點
,射線l與圓C交于點![]() 不同于點
不同于點![]() ,求
,求![]() 面積的最大值.
面積的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,已知橢圓![]() 的離心率為
的離心率為![]() ,右準線方程為
,右準線方程為![]() ,
,![]() 、
、![]() 分別是橢圓
分別是橢圓![]() 的左、右頂點,過右焦點
的左、右頂點,過右焦點![]() 且斜率為
且斜率為![]() 的直線
的直線![]() 與橢圓
與橢圓![]() 相交于
相交于![]() ,
,![]() 兩點.
兩點.
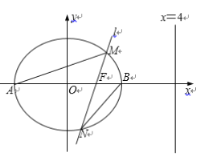
(1)求橢圓![]() 的標準方程.
的標準方程.
(2)記![]() 、
、![]() 的面積分別為
的面積分別為![]() 、
、![]() ,若
,若![]() ,求
,求![]() 的值;
的值;
(3)設線段![]() 的中點為
的中點為![]() ,直線
,直線![]() 與右準線相交于點
與右準線相交于點![]() ,記直線
,記直線![]() 、
、![]() 、
、![]() 的斜率分別為
的斜率分別為![]() 、
、![]() 、
、![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com