
【題目】已知函數![]() (
(![]() ,e是自然對數的底,
,e是自然對數的底,![]() )
)
(1)討論![]() 的單調性;
的單調性;
(2)若![]() ,
,![]() 是函數
是函數![]() 的零點,
的零點,![]() 是
是![]() 的導函數,求證:
的導函數,求證:![]() .
.
【答案】(1)當![]() 時,
時,![]() 在
在![]() 上單調遞減,在
上單調遞減,在![]() 上單調遞增;當
上單調遞增;當![]() 時,
時,![]() 在
在![]() 單調遞增,在
單調遞增,在![]() 上單調遞減,在
上單調遞減,在![]() 上單調遞增; (2)見解析.
上單調遞增; (2)見解析.
【解析】
(1)先求導數,再求導函數零點,再根據![]() 與
與![]() 大小關系分類討論函數單調性,(2)先研究
大小關系分類討論函數單調性,(2)先研究![]() 單調性,轉化所證不等式為
單調性,轉化所證不等式為![]() ,再根據
,再根據![]() 單調性,轉化證明
單調性,轉化證明![]() 且
且![]() .最后利用不等式性質進行論證.
.最后利用不等式性質進行論證.
(1)![]() ,
,
設![]()
![]() ,
,
解法一:由![]() 和
和![]() 在
在![]() 上單調遞增,可知
上單調遞增,可知![]() 在
在![]() 上單調遞增,
上單調遞增,
解法二:由![]() 得
得![]() 可知
可知![]() 在
在![]() 上單調遞增,又
上單調遞增,又![]() ,
,
所以當![]() 時,
時,![]() ,當
,當![]() 時,
時,![]() ,
,
①當![]() 時,
時,![]() ,
,
當![]() 時,
時,![]() ;當
;當![]() 時,
時,![]() .
.
②當![]() 時,由
時,由![]() 得
得![]() 或x=1,
或x=1,
當![]() 時,
時,![]() ,
,![]() ,
,![]() ;
;
當![]() 時,
時,![]() ;當
;當![]() 時,
時,![]() .
.
綜上所述:當![]() 時,
時,![]() 在
在![]() 上單調遞減,在
上單調遞減,在![]() 上單調遞增;
上單調遞增;
當![]() 時,
時,![]() 在
在![]() 單調遞增,在
單調遞增,在![]() 上單調遞減,在
上單調遞減,在![]() 上單調遞增.
上單調遞增.
(2)解法一(分析法):
當![]() 時,由(1)知
時,由(1)知![]() 在
在![]() 上的最大值為
上的最大值為![]() ,
,
可知![]() ,所以
,所以![]() 在
在![]() 上無零點.
上無零點.
若![]() 是函數
是函數![]() 的零點,則
的零點,則![]() ,
,
∵![]() ,
,
解法一:由![]() 和
和![]() 在
在![]() 上單調遞增,且
上單調遞增,且![]() 、
、![]() ,可知
,可知![]() 在
在![]() 上單調遞增,
上單調遞增,
解法二:設![]() ,則
,則![]() ,
,
由![]() 得
得![]() ,
,![]() ,所以
,所以![]() ,
,
可知![]() 在
在![]() 上單調遞增,
上單調遞增,
要證![]() ,只需證
,只需證![]() ,
,
由(1)知![]() 在
在![]() 上單調遞增,
上單調遞增,
只需證![]() ,又
,又![]() ,
,
只需證![]() 且
且![]() .
.
![]()
![]() ,
,
由![]() ,
,![]() ,得
,得![]() ,又
,又![]() ,所以
,所以![]() ;
;
![]() ,由
,由![]() 得
得![]() ,
,
綜上所述,得證.
方法二(綜合法):
當![]() 時,由(1)知
時,由(1)知![]() 在
在![]() 上的最大值為
上的最大值為![]() ,
,
可知![]() ,所以
,所以![]() 在
在![]() 上無零點.
上無零點.
若![]() 是函數
是函數![]() 的零點,則
的零點,則![]() ,
,
而![]()
![]() ,
,
由![]() ,
,![]() ,得
,得![]() ,又
,又![]() ,所以
,所以![]() ;
;
![]() ,由
,由![]() 得
得![]() ,
,
所以![]() ,又
,又![]() ,即
,即![]() ,
,
由(1)知![]() 在
在![]() 上單調遞增,所以
上單調遞增,所以![]() ,
,
而![]() ,
,
由![]() 和
和![]() 在
在![]() 上單調遞增,且
上單調遞增,且![]() 、
、![]() ,
,
可知![]() 在
在![]() 上單調遞增,
上單調遞增,
所以![]() ,得證.
,得證.


科目:高中數學 來源: 題型:
【題目】動點![]() 到直線
到直線![]() 的距離比它到點
的距離比它到點![]() 的距離大1.
的距離大1.
(1)求點![]() 的軌跡
的軌跡![]() 的方程;
的方程;
(2)過定點![]() 作直線
作直線![]() ,與(1)中的軌跡
,與(1)中的軌跡![]() 相交于
相交于![]() 、
、![]() 兩點,
兩點,![]() 為點
為點![]() 關于原點
關于原點![]() 的對稱點,證明:
的對稱點,證明:![]() ;
;
(3)在(2)中,是否存在垂直于![]() 軸的直線
軸的直線![]() 被以
被以![]() 為直徑的圓截得的弦長恒為定值?若存在求出
為直徑的圓截得的弦長恒為定值?若存在求出![]() 的方程;若不存在,請說明理由.
的方程;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】北京地鐵八通線西起四惠站,東至土橋站,全長![]() ,共設13座車站
,共設13座車站![]() 目前八通線執行2014年12月28日制訂的計價標準,各站間計程票價
目前八通線執行2014年12月28日制訂的計價標準,各站間計程票價![]() 單位:元
單位:元![]() 如下:
如下:
四惠 | 3 | 3 | 3 | 3 | 4 | 4 | 4 | 5 | 5 | 5 | 5 | 5 | |
四惠東 | 3 | 3 | 3 | 4 | 4 | 4 | 5 | 5 | 5 | 5 | 5 | ||
高碑店 | 3 | span>3 | 3 | 4 | 4 | 4 | 4 | 5 | 5 | 5 | |||
傳媒大學 | 3 | 3 | 3 | 4 | 4 | 4 | 4 | 5 | 5 | ||||
雙橋 | 3 | 3 | 3 | 4 | 4 | 4 | 4 | 4 | |||||
管莊 | 3 | 3 | 3 | 3 | 4 | 4 | 4 | ||||||
八里橋 | 3 | 3 | 3 | 3 | 4 | 4 | |||||||
通州北苑 | 3 | 3 | 3 | 3 | 3 | ||||||||
果園 | 3 | 3 | 3 | 3 | |||||||||
九棵樹 | 3 | 3 | 3 | ||||||||||
梨園 | 3 | 3 | |||||||||||
臨河里 | 3 | ||||||||||||
土橋 | |||||||||||||
四惠 | 四惠東 | 高碑店 | 傳媒大學 | 雙橋 | 管莊 | 八里橋 | 通州北苑 | 果園 | 九棵樹 | 梨園 | 臨河里 | 土橋 |
![]() 1
1![]() 在13座車站中任選兩個不同的車站,求兩站間票價為5元的概率;
在13座車站中任選兩個不同的車站,求兩站間票價為5元的概率;
![]() 2
2![]() 在土橋出站口隨機調查了n名下車的乘客,將在八通線各站上車情況統計如下表:
在土橋出站口隨機調查了n名下車的乘客,將在八通線各站上車情況統計如下表:
上車站點 | 通州北苑
| 雙橋 | 四惠
|
頻率 |
| a | b |
人數 | c | 15 | 25 |
求a,b,c,n的值,并計算這n名乘客乘車平均消費金額;
![]() 3
3![]() 某人從四惠站上車乘坐八通線到土橋站,中途任選一站出站一次,之后再從該站乘車
某人從四惠站上車乘坐八通線到土橋站,中途任選一站出站一次,之后再從該站乘車![]() 若想兩次乘車花費總金額最少,可以選擇中途哪站下車?
若想兩次乘車花費總金額最少,可以選擇中途哪站下車?![]() 寫出一個即可
寫出一個即可![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖所示:在五面體ABCDEF中,四邊形EDCF是正方形,AD=DE=1,∠ADE=90°,∠ADC=∠DCB=120°.
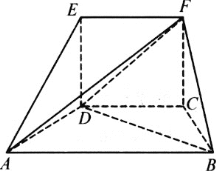
(Ⅰ)求證:平面ABCD⊥平面EDCF;
(Ⅱ)求三棱錐A-BDF的體積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某地種植常規稻A和雜交稻B,常規稻A的畝產穩定為500公斤,統計近年來數據得到每年常規稻A的單價比當年雜交稻B的單價高50%.統計雜交稻B的畝產數據,得到畝產的頻率分布直方圖如下;統計近10年來雜交稻B的單價(單位:元/公斤)與種植畝數(單位:萬畝)的關系,得到的10組數據記為![]() ,并得到散點圖如下,參考數據見下.
,并得到散點圖如下,參考數據見下.
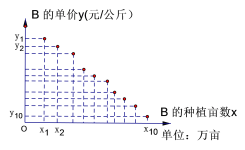
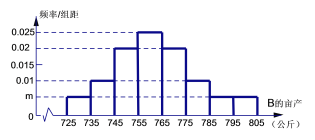
(1)求出頻率分布直方圖中m的值,若各組的取值按中間值來計算,求雜交稻B的畝產平均值;
(2)判斷雜交稻B的單價y(單位:元/公斤)與種植畝數x(單位:萬畝)是否線性相關,若相關,試根據以下統計的參考數據求出y關于x的線性回歸方程;
(3)調查得到明年此地雜交稻B的種植畝數預計為2萬畝,估計明年常規稻A的單價,若在常規稻A和雜交稻B中選擇,明年種植哪種水稻收入更高?
統計參考數據:![]() ,
,![]() ,
,![]() ,
,![]() ,
,
附:線性回歸方程![]() ,
,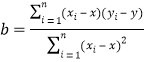 .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
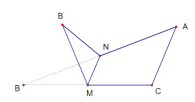
【題目】如圖,∠C=![]() ,
,![]() ,M,N分別是BC,AB的中點,將△BMN沿直線MN折起,使二面角B'-MN-B的大小為
,M,N分別是BC,AB的中點,將△BMN沿直線MN折起,使二面角B'-MN-B的大小為![]() ,則B'N與平面ABC所成角的正切值是( )
,則B'N與平面ABC所成角的正切值是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知拋物線C:y2=2px(p>0)的焦點F,直線y=4與y軸的交點為P,與拋物線C的交點為Q,且|QF|=2|PQ|.
(1)求p的值;
(2)已知點T(t,-2)為C上一點,M,N是C上異于點T的兩點,且滿足直線TM和直線TN的斜率之和為![]() ,證明直線MN恒過定點,并求出定點的坐標.
,證明直線MN恒過定點,并求出定點的坐標.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】![]() 九章算術
九章算術![]() 給出求羨除體積的“術”是:“并三廣,以深乘之,又以袤乘之,六而一”,其中的“廣”指羨除的三條平行側棱的長,“深”指一條側棱到另兩條側棱所在平面的距離,“袤”指這兩條側棱所在平行線之間的距離,用現代語言描述:在羨除
給出求羨除體積的“術”是:“并三廣,以深乘之,又以袤乘之,六而一”,其中的“廣”指羨除的三條平行側棱的長,“深”指一條側棱到另兩條側棱所在平面的距離,“袤”指這兩條側棱所在平行線之間的距離,用現代語言描述:在羨除![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,兩條平行線
,兩條平行線![]() 與
與![]() 間的距離為h,直線
間的距離為h,直線![]() 到平面
到平面![]() 的距離為
的距離為![]() ,則該羨除的體積為
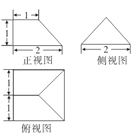
,則該羨除的體積為![]() 已知某羨除的三視圖如圖所示,則該羨除的體積為
已知某羨除的三視圖如圖所示,則該羨除的體積為![]()
![]()
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com