
【題目】已知函數f(x)(x∈R)滿足f(﹣x)=8﹣f(4+x),函數g(x)= ![]() ,若函數f(x)與g(x)的圖象共有168個交點,記作Pi(xi , yi)(i=1,2,…,168),則(x1+y1)+(x2+y2)+…+(x168+y168)的值為( )
,若函數f(x)與g(x)的圖象共有168個交點,記作Pi(xi , yi)(i=1,2,…,168),則(x1+y1)+(x2+y2)+…+(x168+y168)的值為( )
A.2018
B.2017
C.2016
D.1008
 尖子生新課堂課時作業系列答案
尖子生新課堂課時作業系列答案 英才計劃同步課時高效訓練系列答案
英才計劃同步課時高效訓練系列答案科目:高中數學 來源: 題型:
【題目】程序框圖如圖所示,現輸入如下四個函數:f(x)= ![]() ,f(x)=x4 , f(x)=2x , f(x)=x﹣
,f(x)=x4 , f(x)=2x , f(x)=x﹣ ![]() ,則可以輸出的函數是( )
,則可以輸出的函數是( ) 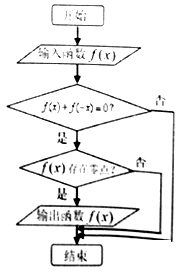
A.f(x)= ![]()
B.f(x)=x4
C.f(x)=2x
D.f(x)=x﹣ ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設f(x)=ax2﹣(a+1)x+1
(1)解關于x的不等式f(x)>0;
(2)若對任意的a∈[﹣1,1],不等式f(x)>0恒成立,求x的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)= ![]() .
.
(1)求f(x)+f(1﹣x)的值;
(2)若數列{an}滿足an=f(0)+f( ![]() )+f(
)+f( ![]() )+…+f(
)+…+f( ![]() )+f(1)(n∈N*),求數列{an}的通項公式;
)+f(1)(n∈N*),求數列{an}的通項公式;
(3)若數列{bn}滿足bn=2nan , Sn是數列{bn}的前n項和,是否存在正實數k,使不等式knSn>3bn對于一切的n∈N*恒成立?若存在,請求出k的取值范圍;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】4月23人是“世界讀書日”,某中學在此期間開展了一系列的讀書教育活動,為了解本校學生課外閱讀情況,學校隨機抽取了100名學生對其課外閱讀時間進行調查,下面是根據調查結果繪制的學生日均課外閱讀時間(單位:分鐘)的頻率分布直方圖,若將日均課外閱讀時間不低于60分鐘的學生稱為“讀書謎”,低于60分鐘的學生稱為“非讀書謎” 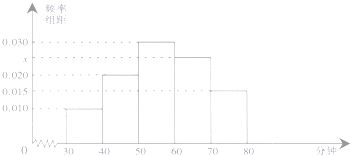
附:K2= ![]() n=a+b+c+d
n=a+b+c+d
P(K2≥k0) | 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
k0 | 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
(1)求x的值并估計全校3000名學生中讀書謎大概有多少?(經頻率視為頻率)
(2)根據已知條件完成下面2×2的列聯表,并據此判斷是否有99%的把握認為“讀書謎”與性別有關?
非讀書迷 | 讀書迷 | 合計 | |
男 | 15 | ||
女 | 45 | ||
合計 |
查看答案和解析>>
科目:高中數學 來源: 題型:
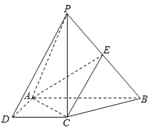
【題目】如圖,在四棱錐![]() 中,
中, ![]() 底面
底面![]() ,底面
,底面![]() 是直角梯形,
是直角梯形, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 是
是![]() 的中點.
的中點.
(1)求證:平面![]() 平面
平面![]() ;
;
(2)若二面角![]() 的余弦值為
的余弦值為![]() ,求直線
,求直線![]() 與平面
與平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知數列{an}中各項都大于1,前n項和為Sn , 且滿足an2+3an=6Sn﹣2.
(1)求數列{an}的通項公式;
(2)令bn= ![]() ,求數列{bn}的前n項和Tn;
,求數列{bn}的前n項和Tn;
(3)求使得Tn< ![]() 對所有n∈N*都成立的最小正整數m.
對所有n∈N*都成立的最小正整數m.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某省的一個氣象站觀測點在連續4天里記錄的![]() 指數
指數![]() 與當天的空氣水平可見度
與當天的空氣水平可見度![]() (單位:
(單位: ![]() )的情況如表1:
)的情況如表1:

該省某市2016年11月![]() 指數頻數分布如表2:
指數頻數分布如表2:
|
|
|
|
|
|
頻數 | 3 | 6 | 12 | 6 | 3 |
(1)設![]() ,根據表1的數據,求出
,根據表1的數據,求出![]() 關于
關于![]() 的線性回歸方程;
的線性回歸方程;
(附參考公式: ![]() ,其中
,其中 ,
, ![]() )
)
(2)小李在該市開了一家洗車店,經統計,洗車店平均每天的收入與![]() 指數由相關關系,如表3:
指數由相關關系,如表3:
|
|
|
|
|
|
日均收入(元) |
|
|
|
|
|
根據表3估計小李的洗車店該月份平均每天的收入.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com