
【題目】△ABC的內角A,B,C的對邊分別為a,b,c.已知asin(A+B)=csin![]() .
.
(1)求A;
(2)求sinBsinC的取值范圍;
(3)若△ABC的面積為![]() ,周長為8,求a.
,周長為8,求a.
【答案】(1)A![]() (2)(0,
(2)(0,![]() )(3)a
)(3)a![]()
【解析】
(1)用誘導公式和正弦定理化邊為角,然后再由二倍角公式變形后可求得![]() ;
;
(2)由(1)可得![]() ,
,![]() ,把
,把![]() 化為
化為![]() 的函數,由三角函數恒等變換化為一個三角函數形式,結合正弦函數性質可得取值范圍;
的函數,由三角函數恒等變換化為一個三角函數形式,結合正弦函數性質可得取值范圍;
(3)由三角形面積可求得![]() ,由周長及余弦定理得
,由周長及余弦定理得![]() 的三個等式,消去
的三個等式,消去![]() 可解得
可解得![]() .
.
(1)△ABC中,asin(A+B)=csin![]() ,
,
∴asin(π﹣C)=csin(![]() ),
),
∴asinC=ccos![]() ,由正弦定理得sinAsinC=sinCcos
,由正弦定理得sinAsinC=sinCcos![]() ,
,
∴sinA=cos![]() ,即2sin
,即2sin![]() cos
cos![]() cos
cos![]() ;
;
又A∈(0,π),
∴cos![]() 0,
0,
∴2sin![]() 1,即sin
1,即sin![]() ,
,
∴![]() ,
,
解得A![]() ;
;
(2)∵sinBsinC=sinBsin(![]() B)
B)![]() sinBcosB
sinBcosB![]() sin2B
sin2B![]() sin2B
sin2B![]() cos2B
cos2B![]() sin(2B
sin(2B![]() )
)![]() ,
,
又∵B∈(0,![]() ),
),
∴2B![]() ∈(
∈(![]() ,
,![]() ),sin(2B
),sin(2B![]() )∈(
)∈(![]() ,1],
,1],
∴sinBsinC∈(0,![]() ).
).
(3)△ABC的面積為![]() ,周長為8,
,周長為8,
∴![]() bcsinA
bcsinA![]() bc
bc![]() ,
,
∴bc=4,…①
a+b+c=8,…②
由余弦定理得:a2=b2+c2﹣bc,…③
由①②③組成方程組,可得: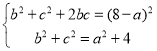 ,
,
可得:(8﹣a)2=a2+12,
解得:a![]() .
.


 輕松課堂單元測試AB卷系列答案
輕松課堂單元測試AB卷系列答案 小題狂做系列答案
小題狂做系列答案科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的離心率為
的離心率為![]() ,以原點為圓心,橢圓
,以原點為圓心,橢圓![]() 的短半軸長為半徑的圓與直線
的短半軸長為半徑的圓與直線![]() 相切.
相切.
(Ⅰ)求橢圓方程;
(Ⅱ)設![]() 為橢圓右頂點,過橢圓
為橢圓右頂點,過橢圓![]() 的右焦點的直線
的右焦點的直線![]() 與橢圓
與橢圓![]() 交于
交于![]() ,
,![]() 兩點(異于
兩點(異于![]() ),直線
),直線![]() ,
,![]() 分別交直線
分別交直線![]() 于
于![]() ,
,![]() 兩點. 求證:
兩點. 求證:![]() ,
,![]() 兩點的縱坐標之積為定值.
兩點的縱坐標之積為定值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在直三棱柱ABC-A1B1C1中,D,E分別為AB,BC的中點,點F在側棱B1B上,且![]() ,
, ![]() .
.

求證:(1)直線DE![]() 平面A1C1F;
平面A1C1F;
(2)平面B1DE⊥平面A1C1F.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,是一個半圓柱與多面體![]() 構成的幾何體,平面
構成的幾何體,平面![]() 與半圓柱的下底面共面,且
與半圓柱的下底面共面,且![]() ,
, ![]() 為弧
為弧![]() 上(不與
上(不與![]() 重合)的動點.
重合)的動點.
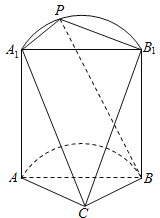
(1)證明: ![]() 平面
平面![]() ;
;
(2)若四邊形![]() 為正方形,且
為正方形,且![]() ,
, ![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】《九章算術》是我國古代內容極為豐富的數學名著,書中將底面為直角三角形且側棱垂直與底面的棱柱稱為塹堵,將底面為矩形的棱臺稱為芻童.在如圖所示的塹堵![]() 與芻童
與芻童![]() 的組合體中,
的組合體中,![]() .
.
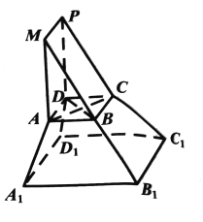
(1)證明:直線![]() 平面
平面![]() ;
;
(2)已知![]() ,且三棱錐A-A1B1D1的體積
,且三棱錐A-A1B1D1的體積![]() ,求該組合體的體積.
,求該組合體的體積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設min{m,n}表示m,n二者中較小的一個,已知函數f(x)=x2+8x+14,g(x)=![]() (x>0),若x1∈[-5,a](a≥-4),x2∈(0,+∞),使得f(x1)=g(x2)成立,則a的最大值為
(x>0),若x1∈[-5,a](a≥-4),x2∈(0,+∞),使得f(x1)=g(x2)成立,則a的最大值為
A.-4B.-3C.-2D.0
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的兩個焦點分別為
的兩個焦點分別為![]() ,長軸長為
,長軸長為![]() .
.
(Ⅰ)求橢圓![]() 的標準方程及離心率;
的標準方程及離心率;
(Ⅱ)過點![]() 的直線
的直線![]() 與橢圓
與橢圓![]() 交于
交于![]() ,
,![]() 兩點,若點
兩點,若點![]() 滿足
滿足![]() ,求證:由點
,求證:由點![]() 構成的曲線
構成的曲線![]() 關于直線
關于直線![]() 對稱.
對稱.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知冪函數![]() 在(0,+∞)上單調遞增,函數g(x)=2x-k.
在(0,+∞)上單調遞增,函數g(x)=2x-k.
(1)求m的值;
(2)當x∈[1,2)時,記f(x),g(x)的值域分別為集合A,B,設p:x∈A,q:x∈B,若p是q成立的必要條件,求實數k的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com