
【題目】已知函數![]() ,其中
,其中![]() ,
,![]() 為自然對數的底數.
為自然對數的底數.
(1)若![]() ,求函數
,求函數![]() 在
在![]() 處的切線方程;
處的切線方程;
(2)若函數![]() 在定義域上恰有兩個不同的零點,求實數a的取值范圍;
在定義域上恰有兩個不同的零點,求實數a的取值范圍;
(3)設函數![]() 在區間
在區間![]() )上存在極值,求證:
)上存在極值,求證:![]() .
.
【答案】(1)![]() (2)
(2)![]() 或
或![]() (3)證明見解析
(3)證明見解析
【解析】
(1)利用導數求函數![]() 在
在![]() 處的切線方程;(2)對
處的切線方程;(2)對![]() 分
分![]() 兩種情況討論,當
兩種情況討論,當![]() 時,再分三種情況結合導數分類討論;(3)先求出
時,再分三種情況結合導數分類討論;(3)先求出![]() ,要使得
,要使得![]() 在
在![]() 上存在極值,則須滿足
上存在極值,則須滿足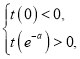 即
即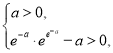 分析推理即可得到
分析推理即可得到![]() .
.
(1)當![]() 時,
時,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
所以函數![]() 在
在![]() 處得切線方程為
處得切線方程為![]() .
.
(2)因為![]() ,
,![]() ,
,![]() ,
,
所以![]() .
.
①若![]() ,則
,則![]() ,
,![]() 在
在![]() 上是單調增函數,
上是單調增函數,
所以![]() 在
在![]() 上至多一個零點,與題意不符合.
上至多一個零點,與題意不符合.
②若![]() ,令
,令![]() ,得
,得![]() .
.
|
|
|
|
|
| 0 |
|
|
| 極小值 |
|
(ⅰ)若![]() ,即
,即![]() 時,
時,![]() 有且僅有一個零點
有且僅有一個零點![]() ,與題意不符.
,與題意不符.
(ⅱ)若![]() ,即
,即![]() 時,
時,![]() ,
,![]() ,
,
又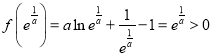 ,且
,且![]() 的圖像在
的圖像在![]() 上不間斷,
上不間斷,
所以存在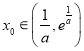 ,使得
,使得![]() .
.
此時,![]() 在
在![]() 恰有兩個不同得零點
恰有兩個不同得零點![]() 和
和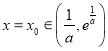 .
.
所以![]() 符合題意.
符合題意.
(ⅲ)若![]() ,即
,即![]() 時,
時,![]() .
.
令![]() ,
,![]() ,
,![]() ,
,
所以![]() 在
在![]() 上是單調增函數,
上是單調增函數,![]() ,
,
所以![]() 在
在![]() 上是單調增函數,
上是單調增函數,![]() .
.
所以![]() ,且
,且![]() ,
,![]() 的圖像在
的圖像在![]() 上不間斷,
上不間斷,
所以存在![]() ,使得
,使得![]() .
.
此時,![]() 在
在![]() 恰有兩個不同得零點
恰有兩個不同得零點![]() 和
和![]() .
.
所以![]() 符合題意.
符合題意.
綜上所述,實數![]() 的取值范圍是
的取值范圍是![]() 或
或![]() .
.
(3)依題意![]() ,
,![]() .
.
則![]() ,令
,令![]() ,
,![]() ,
,![]() ,
,
所以![]() 在
在![]() 上是單調增函數.
上是單調增函數.
要使得![]() 在
在![]() 上存在極值,
上存在極值,
則須滿足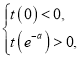 即
即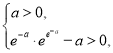
所以![]() ,
,![]() ,即
,即![]() .
.
由(2)可知,當![]() 時,
時,![]() ,
,
所以![]() ,
,![]() .
.
所以![]() ,即
,即![]() ,
,
所以![]() .
.


科目:高中數學 來源: 題型:
【題目】在①![]() ,②
,②![]() ,③
,③![]() 這三個條件中任選一個,補充在下面的問題中,并解決該問題.
這三個條件中任選一個,補充在下面的問題中,并解決該問題.
已知![]() 的內角
的內角![]() ,
,![]() ,
,![]() 的對邊分別為
的對邊分別為![]() ,
,![]() ,
,![]() ______________,
______________,![]() ,
,![]() ,求
,求![]() 的面積.
的面積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】改編自中國神話故事的動畫電影《哪吒之魔童降世》自7月26日首映,在不到一個月的時間,票房收入就超過了38億元,創造了中國動畫電影的神話.小明和同學相約去電影院觀看《哪吒之魔童降世》,影院的三個放映廳分別在7:30,8:00,8:30開始放映,小明和同學大約在7:40至8:30之間到達影院,且他們到達影院的時間是隨機的,那么他們到達后等待的時間不超過10分鐘的概率是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2019年是新中國成立七十周年,新中國成立以來,我國文化事業得到了充分發展,尤其是黨的十八大以來,文化事業發展更加迅速,下圖是從2013 年到 2018 年六年間我國公共圖書館業機構數(個)與對應年份編號的散點圖(為便于計算,將 2013 年編號為 1,2014 年編號為 2,…,2018年編號為 6,把每年的公共圖書館業機構個數作為因變量,把年份編號從 1 到 6 作為自變量進行回歸分析),得到回歸直線![]() ,其相關指數
,其相關指數![]() ,給出下列結論,其中正確的個數是( )
,給出下列結論,其中正確的個數是( )

①公共圖書館業機構數與年份的正相關性較強
②公共圖書館業機構數平均每年增加13.743個
③可預測 2019 年公共圖書館業機構數約為3192個
A.0B.1C.2D.3
查看答案和解析>>
科目:高中數學 來源: 題型:
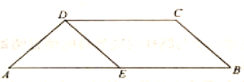
【題目】如圖所示,在等腰梯形![]() 中,
中,![]() ,
,![]() ,
,![]() ,點
,點![]() 為
為![]() 的中點.將
的中點.將![]() 沿
沿![]() 折起,使點
折起,使點![]() 到達
到達![]() 的位置,得到如圖所示的四棱錐
的位置,得到如圖所示的四棱錐![]() ,點
,點![]() 為棱
為棱![]() 的中點.
的中點.
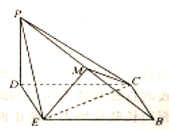
(1)求證:![]() 平面
平面![]() ;
;
(2)若平面![]() 平面
平面![]() ,求三棱錐
,求三棱錐![]() 的體積.
的體積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知拋物線![]() ,
,![]() 、
、![]() 、
、![]() 為拋物線
為拋物線![]() 上不同的三點.
上不同的三點.
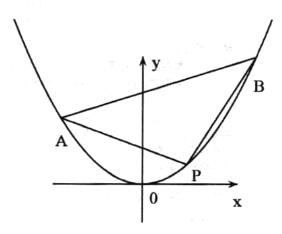
(1)當點![]() 的坐標為
的坐標為![]() 時,若直線
時,若直線![]() 過拋物線焦點
過拋物線焦點![]() 且斜率為
且斜率為![]() ,求直線
,求直線![]() 、
、![]() 斜率之積;
斜率之積;
(2)若![]() 為以
為以![]() 為頂點的等腰直角三角形,求
為頂點的等腰直角三角形,求![]() 面積的最小值.
面積的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某大學生在開學季準備銷售一種文具盒進行試創業,在一個開學季內,每售出![]() 盒該產品獲利潤
盒該產品獲利潤![]() 元,未售出的產品,每盒虧損
元,未售出的產品,每盒虧損![]() 元.根據歷史資料,得到開學季市場需求量的頻率分布直方圖,如圖所示.該同學為這個開學季購進了
元.根據歷史資料,得到開學季市場需求量的頻率分布直方圖,如圖所示.該同學為這個開學季購進了![]() 盒該產品,以
盒該產品,以![]() (單位:盒,
(單位:盒,![]() )表示這個開學季內的市場需求量,
)表示這個開學季內的市場需求量,![]() (單位:元)表示這個開學季內經銷該產品的利潤.
(單位:元)表示這個開學季內經銷該產品的利潤.

(1)根據直方圖估計這個開學季內市場需求量![]() 的眾數和平均數;
的眾數和平均數;
(2)將![]() 表示為
表示為![]() 的函數;
的函數;
(3)根據直方圖估計利潤![]() 不少于
不少于![]() 元的概率.
元的概率.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com