
【題目】新能源汽車是戰略性新興行業之一,發展新能源汽車是中國從汽車大國邁向汽車強國的必由之路,某汽車企業為了適應市場需求引進了新能源汽車生產設備,2019年該企業新能源汽車的銷售量逐月平穩增長,1,2,3月份的銷售量分別為1.2千臺,1.4千臺,1.8千臺,為估計以后每個月的銷售量,以這三個月的銷售量為依據,用一個函數模擬汽車的月銷售量![]() (單位:千臺)和月份
(單位:千臺)和月份![]() 之間的函數關系,有以下兩個函數模型可供選擇:
之間的函數關系,有以下兩個函數模型可供選擇:
①![]() ;②
;②![]() ,如果4月份的銷售量為2.3千臺,選擇一個效果較好的函數進行模擬,則估計5月份的銷售量為________千臺.
,如果4月份的銷售量為2.3千臺,選擇一個效果較好的函數進行模擬,則估計5月份的銷售量為________千臺.
科目:高中數學 來源: 題型:
【題目】2018年是中國改革開放的第40周年,為了充分認識新形勢下改革開放的時代性,某地的民調機構隨機選取了該地的100名市民進行調查,將他們的年齡分成6段:![]() ,并繪制了如圖所示的頻率分布直方圖.
,并繪制了如圖所示的頻率分布直方圖.

(1)現從年齡在![]() 內的人員中按分層抽樣的方法抽取8人,再從這8人中隨機抽取3人進行座談,用
內的人員中按分層抽樣的方法抽取8人,再從這8人中隨機抽取3人進行座談,用![]() 表示年齡在
表示年齡在![]() 內的人數,求
內的人數,求![]() 的分布列和數學期望;
的分布列和數學期望;
(2)若用樣本的頻率代替概率,用隨機抽樣的方法從該地抽取20名市民進行調查,其中有![]() 名市民的年齡在
名市民的年齡在![]() 的概率為
的概率為![]() .當
.當![]() 最大時,求
最大時,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() :
:![]() 過點
過點![]() ,過坐標原點
,過坐標原點![]() 作兩條互相垂直的射線與橢圓
作兩條互相垂直的射線與橢圓![]() 分別交于
分別交于![]() ,
,![]() 兩點.
兩點.
(1)證明:當![]() 取得最小值時,橢圓
取得最小值時,橢圓![]() 的離心率為
的離心率為![]() .
.
(2)若橢圓![]() 的焦距為2,是否存在定圓與直線
的焦距為2,是否存在定圓與直線![]() 總相切?若存在,求定圓的方程;若不存在,請說明理由.
總相切?若存在,求定圓的方程;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,四邊形ABCD是正方形,PA![]() 平面ABCD,EB//PA,AB=PA=4,EB=2,F為PD的中點.
平面ABCD,EB//PA,AB=PA=4,EB=2,F為PD的中點.
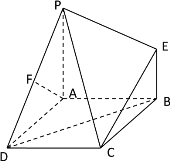
(1)求證AF![]() PC
PC
(2)BD//平面PEC
(3)求二面角D-PC-E的大小
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某地環保部門跟蹤調查一種有害昆蟲的數量.根據調查數據,該昆蟲的數量![]() (萬只)與時間
(萬只)與時間![]() (年)(其中
(年)(其中![]() )的關系為
)的關系為![]() .為有效控制有害昆蟲數量、保護生態環境,環保部門通過實時監控比值
.為有效控制有害昆蟲數量、保護生態環境,環保部門通過實時監控比值![]() (其中
(其中![]() 為常數,且
為常數,且![]() )來進行生態環境分析.
)來進行生態環境分析.
(1)當![]() 時,求比值
時,求比值![]() 取最小值時
取最小值時![]() 的值;
的值;
(2)經過調查,環保部門發現:當比值![]() 不超過
不超過![]() 時不需要進行環境防護.為確保恰好3年不需要進行保護,求實數
時不需要進行環境防護.為確保恰好3年不需要進行保護,求實數![]() 的取值范圍.(
的取值范圍.(![]() 為自然對數的底,
為自然對數的底, ![]() )
)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,已知扇形![]() 是一個觀光區的平面示意圖,其中扇形半徑為10米,
是一個觀光區的平面示意圖,其中扇形半徑為10米,![]() ,為了便于游客觀光和旅游,提出以下兩種設計方案:
,為了便于游客觀光和旅游,提出以下兩種設計方案:
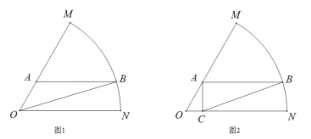
(1)如圖1,擬在觀光區內規劃一條三角形![]() 形狀的道路,道路的一個頂點
形狀的道路,道路的一個頂點![]() 在弧
在弧![]() 上,另一頂點
上,另一頂點![]() 在半徑
在半徑![]() 上,且
上,且![]() ,求
,求![]() 周長的最大值;
周長的最大值;
(2)如圖2,擬在觀光區內規劃一個三角形區域種植花卉,三角形花圃![]() 的一個頂點
的一個頂點![]() 在弧
在弧![]() 上,另兩個頂點
上,另兩個頂點![]()
![]() 在半徑
在半徑![]()
![]() 上,且
上,且![]() ,
,![]() ,求花圃
,求花圃![]() 面積的最大值.
面積的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某廠生產某產品的年固定成本為250萬元,每生產![]() 千件,需另投入成本
千件,需另投入成本![]() (萬元),若年產量不足
(萬元),若年產量不足![]() 千件,
千件, ![]() 的圖像是如圖的拋物線,此時
的圖像是如圖的拋物線,此時![]() 的解集為
的解集為![]() ,且
,且![]() 的最小值是
的最小值是![]() ,若年產量不小于
,若年產量不小于![]() 千件,
千件, ![]() ,每千件商品售價為50萬元,通過市場分析,該廠生產的商品能全部售完;
,每千件商品售價為50萬元,通過市場分析,該廠生產的商品能全部售完;
(1)寫出年利潤![]() (萬元)關于年產量
(萬元)關于年產量![]() (千件)的函數解析式;
(千件)的函數解析式;
(2)年產量為多少千件時,該廠在這一商品的生產中所獲利潤最大?

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】至2018年底,我國發明專利申請量已經連續8年位居世界首位,下表是我國2012年至2018年發明專利申請量以及相關數據.
總計 | ||||||||
年代代碼 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 28 |
申請量 | 65 | 82 | 92 | 110 | 133 | 138 | 154 | 774 |
| 65 | 164 | 276 | 440 | 665 | 828 | 1078 | 3516 |
注:年代代碼1~7分別表示2012~2018.
(1)可以看出申請量每年都在增加,請問這幾年中那一年的增長率達到最高,最高是多少?
(2)建立![]() 關于
關于![]() 的回歸直線方程(精確到0.01),并預測我國發明專利申請量突破200萬件的年份.
的回歸直線方程(精確到0.01),并預測我國發明專利申請量突破200萬件的年份.
參考公式: .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com