
【題目】某休閑農莊有一塊長方形魚塘ABCD,AB=50米,BC=25 ![]() 米,為了便于游客休閑散步,該農莊決定在魚塘內建三條如圖所示的觀光走廊OE、EF和OF,考慮到整體規劃,要求O是AB的中點,點E在邊BC上,點F在邊AD上,且∠EOF=90°.
米,為了便于游客休閑散步,該農莊決定在魚塘內建三條如圖所示的觀光走廊OE、EF和OF,考慮到整體規劃,要求O是AB的中點,點E在邊BC上,點F在邊AD上,且∠EOF=90°. 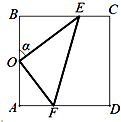
(1)設∠BOE=α,試將△OEF的周長l表示成α的函數關系式,并求出此函數的定義域;
(2)經核算,三條走廊每米建設費用均為4000元,試問如何設計才能使建設總費用最低并求出最低總費用.
【答案】
(1)解:∵在Rt△BOE中,OB=25,∠B=90°,∠BOE=α,
∴OE= ![]()
在Rt△AOF中,OA=25,∠A=90°,∠AFO=α,
∴OF= ![]() .
.
又∠EOF=90°,
∴EF= ![]() =
= ![]() ,
,
∴l=OE+OF+EF= ![]() .
.
當點F在點D時,這時角α最小,此時α= ![]() ;
;
當點E在C點時,這時角α最大,求得此時α= ![]() .
.
故此函數的定義域為[ ![]() ,
, ![]() ];
];
(2)解:由題意知,要求鋪路總費用最低,只要求△OEF的周長l的最小值即可.
由(1)得,l= ![]() ,α∈[
,α∈[ ![]() ,
, ![]() ],
],
設sinα+cosα=t,則sinαcosα= ![]() ,
,
∴l= ![]() =
= ![]()
由t=sinα+cosα= ![]() sin(α+
sin(α+ ![]() ),
),
又 ![]() ≤α+
≤α+ ![]() ≤
≤ ![]() ,得
,得 ![]() ,
,
∴ ![]() ,
,
從而當α= ![]() ,即BE=25時,lmin=50(
,即BE=25時,lmin=50( ![]() +1),
+1),
所以當BE=AF=25米時,鋪路總費用最低,最低總費用為200000( ![]() +1)元
+1)元
【解析】(1)要將△OEF的周長l表示成α的函數關系式,需把△OEF的三邊分別用含有α的關系式來表示,而OE,OF,分別可以在Rt△OBE,Rt△OAF中求解,利用勾股定理可求EF,從而可求.(2)要求鋪路總費用最低,只要求△OEF的周長l的最小值即可.由(1)得l= ![]() ,α∈[
,α∈[ ![]() ,
, ![]() ],利用換元,設sinα+cosα=t,則sinαcosα=
],利用換元,設sinα+cosα=t,則sinαcosα= ![]() ,從而轉化為求函數在閉區間上的最小值.
,從而轉化為求函數在閉區間上的最小值.


科目:高中數學 來源: 題型:
【題目】已知函數f(x)=2sin( ![]() ﹣φ)(0<φ<
﹣φ)(0<φ< ![]() )的圖象經過點(0,﹣1).
)的圖象經過點(0,﹣1).
(1)求函數f(x)的對稱軸方程及相鄰兩條對稱軸間的距離d;
(2)設α、β∈[0, ![]() ],f(3α+
],f(3α+ ![]() )=
)= ![]() ,f(3β+2π)=
,f(3β+2π)= ![]() ,求cos(α+β)的值.
,求cos(α+β)的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() ,
,![]() .
.
(1).當![]() 時,求
時,求![]() 的單調增區間;
的單調增區間;
(2)當![]() ,對于任意
,對于任意![]() ,都有
,都有![]() ,求實數
,求實數![]() 的取值范圍;
的取值范圍;
(3)若函數![]() 的圖象始終在直線
的圖象始終在直線![]() 的下方,求實數
的下方,求實數![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知正項數列{an}的前n項和為Sn,且滿足a1=2,anan+1=2(Sn+1) (![]() ).
).
(1)求數列{an}的通項公式;
(2)若數列{bn}滿足b1=1,![]() (
(![]() ,
,![]() ),求{bn}的前n項和Tn;
),求{bn}的前n項和Tn;
(3)若數列{cn}滿足![]() ,
,![]() (
(![]() ,
,![]() ),試問是否存在正整數p,q(其中1 < p < q),使c1,cp,cq成等比數列?若存在,求出所有滿足條件的數組(p,q);若不存在,說明理由.
),試問是否存在正整數p,q(其中1 < p < q),使c1,cp,cq成等比數列?若存在,求出所有滿足條件的數組(p,q);若不存在,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=(x+1)ln x-a(x-1).
(1)當a=4時,求曲線y=f(x)在(1,f(1))處的切線方程;
(2)若當x∈(1,+∞)時,f(x)>0恒成立,求a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】學校為測評班級學生對任課教師的滿意度,采用“100分制”打分的方式來計分.現從某班學生中隨機抽取10名,以下莖葉圖記錄了他們對某教師的滿意度分數(以十位數字為莖,個位數字為葉):
規定若滿意度不低于98分,測評價該教師為“優秀”.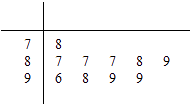
(1)求從這10人中隨機選取3人,至多有1人評價該教師是“優秀”的概率;
記ξ表示抽到評價該教師為“優秀”的人數,求ξ的分布列及數學期望.
(2)以這10人的樣本數據來估計整個班級的總體數據,若從該班任選3人,
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com