
【題目】已知函數f(x)=(x+1)ln x-a(x-1).
(1)當a=4時,求曲線y=f(x)在(1,f(1))處的切線方程;
(2)若當x∈(1,+∞)時,f(x)>0恒成立,求a的取值范圍.
【答案】(1)2x+y-2=0.(2)(-∞,2].
【解析】試題分析:(1)根據導數幾何意義得f′(1)=k,再根據點斜式求切線方程(2)不等式恒成立問題一般轉化為對應函數最值問題:![]() ,利用導數可得函數單調性:為單調遞增,再利用洛必達法則得
,利用導數可得函數單調性:為單調遞增,再利用洛必達法則得![]() ,即得
,即得![]() 的取值范圍
的取值范圍
試題解析:解 (1)f(x)的定義域為(0,+∞).當a=4時,
f(x)=(x+1)ln x-4(x-1),f′(x)=ln x+![]() -3,f′(1)=-2,f(1)=0.
-3,f′(1)=-2,f(1)=0.
故曲線y=f(x)在(1,f(1))處的切線方程為2x+y-2=0.
(2)當x∈(1,+∞)時,f(x)>0等價于ln x-![]() >0.
>0.
設g(x)=ln x-![]() ,則g′(x)=
,則g′(x)=![]() -
-![]() =
=![]() ,g(1)=0.
,g(1)=0.
(i)當a≤2,x∈(1,+∞)時,x2+2(1-a)x+1≥x2-2x+1>0,故g′(x)>0,
g(x)在(1,+∞)上單調遞增,因此g(x)>0.
(ii)當a>2時,令g′(x)=0,得x1=a-1-![]() ,x2=a-1+
,x2=a-1+![]() .
.
由x2>1和x1x2=1得x1<1,故當x∈(1,x2)時,g′(x)<0,g(x)在(1,x2)上單調遞減,因此g(x)<0.
綜上,a的取值范圍是(-∞,2].


科目:高中數學 來源: 題型:
【題目】已知向量 ![]() =(
=( ![]() sinx,﹣1),
sinx,﹣1), ![]() =(cosx,m),m∈R.
=(cosx,m),m∈R.
(1)若m= ![]() ,且
,且 ![]() ∥
∥ ![]() ,求
,求 ![]() 的值;
的值;
(2)已知函數f(x)=2( ![]() +
+ ![]() )
) ![]() ﹣2m2﹣1,若函數f(x)在[0,
﹣2m2﹣1,若函數f(x)在[0, ![]() ]上有零點,求m的取值范圍.
]上有零點,求m的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設f(n)是定義在N*上的增函數,f(4)=5,且滿足:
①任意n∈N*,f(n)![]() Z;②任意m,n∈N*,有f(m)f(n)=f(mn)+f(m+n-1).
Z;②任意m,n∈N*,有f(m)f(n)=f(mn)+f(m+n-1).
(1)求f(1),f(2),f(3)的值;
(2)求f(n)的表達式.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某休閑農莊有一塊長方形魚塘ABCD,AB=50米,BC=25 ![]() 米,為了便于游客休閑散步,該農莊決定在魚塘內建三條如圖所示的觀光走廊OE、EF和OF,考慮到整體規劃,要求O是AB的中點,點E在邊BC上,點F在邊AD上,且∠EOF=90°.
米,為了便于游客休閑散步,該農莊決定在魚塘內建三條如圖所示的觀光走廊OE、EF和OF,考慮到整體規劃,要求O是AB的中點,點E在邊BC上,點F在邊AD上,且∠EOF=90°. 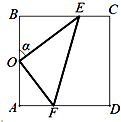
(1)設∠BOE=α,試將△OEF的周長l表示成α的函數關系式,并求出此函數的定義域;
(2)經核算,三條走廊每米建設費用均為4000元,試問如何設計才能使建設總費用最低并求出最低總費用.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知圓心(a,b)(a<0,b<0)在直線y=2x+1上的圓,若其圓心到x軸的距離恰好等于圓的半徑,在y軸上截得的弦長為 ![]() ,則圓的方程為( )
,則圓的方程為( )
A.(x+2)2+(y+3)2=9
B.(x+3)2+(y+5)2=25
C.![]()
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】對兩個變量y和x進行回歸分析,得到一組樣本數據:(x1 , y1),(x2 , y2),…,(xn , yn),則下列說法中不正確的是( )
A.由樣本數據得到的回歸方程 ![]() =
= ![]() x+
x+ ![]() 必過樣本中心(
必過樣本中心( ![]() ,
, ![]() )
)
B.殘差平方和越小的模型,擬合的效果越好
C.用相關指數R2來刻畫回歸效果,R2越小,說明模型的擬合效果越好
D.兩個隨機變量的線性相關性越強,相關系數的絕對值越接近于1
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,直角![]() 中,∠
中,∠![]() ,
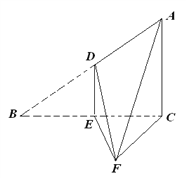
,![]() ,D、E分別是AB、BC邊的中點,沿DE將
,D、E分別是AB、BC邊的中點,沿DE將![]() 折起至
折起至![]() ,且∠
,且∠![]() .
.
(Ⅰ)求四棱錐F-ADEC的體積;
(Ⅱ)求證:平面ADF⊥平面ACF.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某學校為了解高三年級學生寒假期間的學習情況,抽取甲、乙兩班,調查這兩個班的學生在寒假期間每天平均學習的時間(單位:小時),統計結果繪成頻率分布直方圖(如圖).已知甲、乙兩班學生人數相同,甲班學生每天平均學習時間在區間[2,4]的有8人.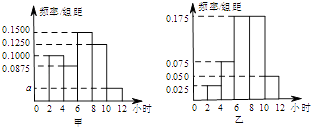
(1)求直方圖中a的值及甲班學生每天平均學習時間在區間(10,12]的人數;
(2)從甲、乙兩個班每天平均學習時間大于10個小時的學生中任取4人參加測試,設4人中甲班學生的人數為ξ,求ξ的分布列和數學期望.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com