
設函數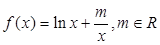 .
.
(1)當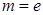 (
(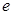 為自然對數的底數)時,求
為自然對數的底數)時,求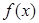 的最小值;
的最小值;
(2)討論函數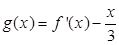 零點的個數;
零點的個數;
(3)若對任意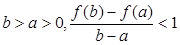 恒成立,求
恒成立,求 的取值范圍.
的取值范圍.
(1)2;(2)當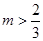 時,函數
時,函數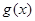 無零點;當
無零點;當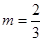 或
或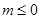 時,函數
時,函數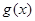 有且僅有一個零點;當
有且僅有一個零點;當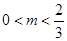 時,函數
時,函數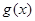 有兩個零點;(3)
有兩個零點;(3)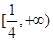 .
.
解析試題分析:(1)當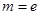 時,
時,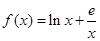 ,易得函數
,易得函數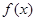 的定義域為
的定義域為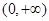 ,求出導函數
,求出導函數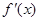 ,利用
,利用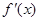 判定函數
判定函數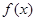 在定義區間內的單調性,并求出
在定義區間內的單調性,并求出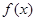 的極小值;
的極小值;
(2)由函數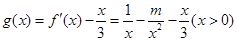 ,令
,令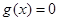 ,得
,得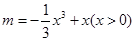 ,
,
設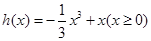 ,由
,由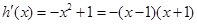 求出函數
求出函數 的單調性以及極值,并且求出函數
的單調性以及極值,并且求出函數 在
在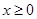 的零點,畫出
的零點,畫出 的大致圖像,并從圖像中,可以得知,當
的大致圖像,并從圖像中,可以得知,當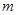 在不同范圍的時候,函數
在不同范圍的時候,函數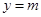 和函數
和函數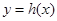 的交點個數
的交點個數
(3)對任意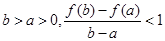 恒成立,等價于
恒成立,等價于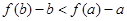 恒成立,則
恒成立,則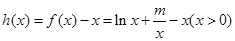 在
在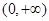 上單調遞減,即
上單調遞減,即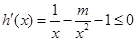 在
在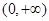 恒成立,
恒成立,
求出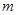 的取值范圍.
的取值范圍.
試題解析:(1)當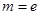 時,
時,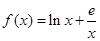
易得函數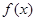 的定義域為
的定義域為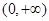
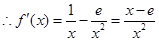
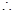 當
當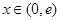 時,
時,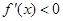 ,此時
,此時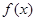 在
在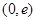 上是減函數;
上是減函數;
當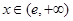 時,
時,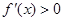 ,此時
,此時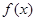 在
在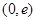 上是增函數;
上是增函數;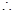 當
當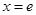 時,
時,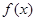 取得極小值
取得極小值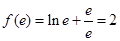
(2) 函數
函數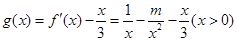
令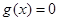 ,得
,得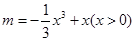
設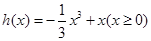
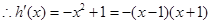
當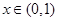 時,
時,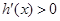 ,此時
,此時 在
在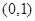 上式增函數;
上式增函數;
當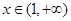 時,
時,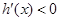 ,此時
,此時 在
在 上式增函數;
上式增函數;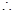 當
當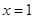 時,
時, 取極大值
取極大值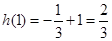
令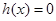 ,即
,即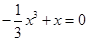 ,解得
,解得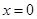


科目:高中數學 來源: 題型:解答題
用白鐵皮做一個平底、圓錐形蓋的圓柱形糧囤,糧囤容積為 (不含錐形蓋內空間),蓋子的母線與底面圓半徑的夾角為
(不含錐形蓋內空間),蓋子的母線與底面圓半徑的夾角為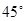 ,設糧囤的底面圓半徑為R
,設糧囤的底面圓半徑為R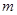 ,需用白鐵皮的面積記為
,需用白鐵皮的面積記為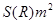 (不計接頭等)。
(不計接頭等)。
(1)將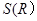 表示為R的函數;
表示為R的函數;
(2)求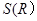 的最小值及對應的糧囤的總高度。(含圓錐頂蓋)
的最小值及對應的糧囤的總高度。(含圓錐頂蓋)
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
已知函數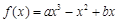 (
(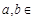 R),
R),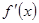 為其導函數,且
為其導函數,且 時
時 有極小值
有極小值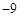 .
.
(1)求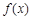 的單調遞減區間;
的單調遞減區間;
(2)若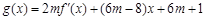 ,
,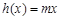 ,當
,當 時,對于任意x,
時,對于任意x,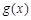 和
和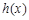 的值至少有一個是正數,求實數m的取值范圍;
的值至少有一個是正數,求實數m的取值范圍;
(3)若不等式 (
( 為正整數)對任意正實數
為正整數)對任意正實數 恒成立,求
恒成立,求 的最大值.
的最大值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com