
【題目】如圖,在多面體![]() 中,四邊形
中,四邊形![]() 為正方形,
為正方形,![]() ,
,![]() ,
,![]() .
.
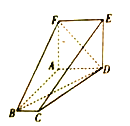
(1)證明:平面![]() 平面
平面![]() .
.
(2)若![]() 平面
平面![]() ,二面角
,二面角![]() 為
為![]() ,三棱錐
,三棱錐![]() 的外接球的球心為
的外接球的球心為![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
【答案】(1)詳見解析;(2)![]() .
.
【解析】
證明![]() 平面
平面![]() 即可證明平面
即可證明平面![]() 平面
平面![]() (2)由題確定二面角
(2)由題確定二面角![]() 的平面角為
的平面角為![]() ,進而推出
,進而推出![]() 為線段
為線段![]() 的中點,以
的中點,以![]() 為坐標(biāo)原點建立空間直角坐標(biāo)系
為坐標(biāo)原點建立空間直角坐標(biāo)系![]() 由空間向量的線面角公式求解即可
由空間向量的線面角公式求解即可
(1)證明:因為四邊形![]() 為正方形,
為正方形,
所以![]() ,
,
又![]() ,
,![]() ,
,
所以![]() 平面
平面![]() .
.
因為![]() 平面
平面![]() ,所以平面
,所以平面![]() 平面
平面![]() .
.
(2)解:由(1)知![]() 平面
平面![]() ,又
,又![]() ,則
,則![]() 平面
平面![]() ,從而
,從而![]() ,
,
又![]() ,所以二面角
,所以二面角![]() 的平面角為
的平面角為![]() .
.
以![]() 為坐標(biāo)原點建立空間直角坐標(biāo)系
為坐標(biāo)原點建立空間直角坐標(biāo)系![]() ,如圖所示,
,如圖所示,
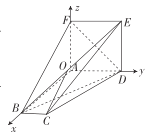
則![]() ,
,![]() ,
,![]() .
.
因為三棱錐![]() 的外接球的球心為
的外接球的球心為![]() ,所以
,所以![]() 為線段
為線段![]() 的中點,
的中點,
則![]() 的坐標(biāo)為
的坐標(biāo)為![]() ,
,![]() .
.
設(shè)平面![]() 的法向量為
的法向量為![]() ,則
,則![]() ,
,
即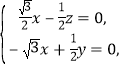 令
令![]() ,得
,得![]() .
.
易知平面![]() 的一個法向量為
的一個法向量為![]() ,
,
則![]() .
.
由圖可知,二面角![]() 為銳角,
為銳角,
故二面角![]() 的余弦值為
的余弦值為![]() .
.


 全能測控期末小狀元系列答案
全能測控期末小狀元系列答案科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知動圓P恒過定點![]() ,且與直線
,且與直線![]() 相切.
相切.
(Ⅰ)求動圓P圓心的軌跡M的方程;
(Ⅱ)正方形ABCD中,一條邊AB在直線y=x+4上,另外兩點C、D在軌跡M上,求正方形的面積.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】當(dāng)前,以“立德樹人”為目標(biāo)的課程改革正在有序推進.高中聯(lián)招對初三畢業(yè)學(xué)生進行體育測試,是激發(fā)學(xué)生、家長和學(xué)校積極開展體育活動,保證學(xué)生健康成長的有效措施.程度2019年初中畢業(yè)生升學(xué)體育考試規(guī)定,考生必須參加立定跳遠、擲實心球、1分鐘跳繩三項測試,三項考試滿分50分,其中立定跳遠15分,擲實心球15分,1分鐘跳繩20分.某學(xué)校在初三上期開始時要掌握全年級學(xué)生每分鐘跳繩的情況,隨機抽取了100名學(xué)生進行測試,得到下邊頻率分布直方圖,且規(guī)定計分規(guī)則如下表:
每分鐘跳繩個數(shù) |
|
|
|
|
得分 | 17 | 18 | 19 | 20 |
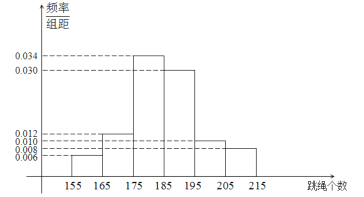
(Ⅰ)現(xiàn)從樣本的100名學(xué)生中,任意選取2人,求兩人得分之和不大于35分的概率;;
(Ⅱ)若該校初三年級所有學(xué)生的跳繩個數(shù)![]() 服從正態(tài)分布
服從正態(tài)分布![]() ,用樣本數(shù)據(jù)的平均值和方差估計總體的期望和方差,已知樣本方差
,用樣本數(shù)據(jù)的平均值和方差估計總體的期望和方差,已知樣本方差![]() (各組數(shù)據(jù)用中點值代替).根據(jù)往年經(jīng)驗,該校初三年級學(xué)生經(jīng)過一年的訓(xùn)練,正式測試時每人每分鐘跳繩個數(shù)都有明顯進步,假設(shè)今年正式測試時每人每分鐘跳繩個數(shù)比初三上學(xué)期開始時個數(shù)增加10個,現(xiàn)利用所得正態(tài)分布模型:
(各組數(shù)據(jù)用中點值代替).根據(jù)往年經(jīng)驗,該校初三年級學(xué)生經(jīng)過一年的訓(xùn)練,正式測試時每人每分鐘跳繩個數(shù)都有明顯進步,假設(shè)今年正式測試時每人每分鐘跳繩個數(shù)比初三上學(xué)期開始時個數(shù)增加10個,現(xiàn)利用所得正態(tài)分布模型:
![]() 預(yù)計全年級恰有2000名學(xué)生,正式測試每分鐘跳182個以上的人數(shù);(結(jié)果四舍五入到整數(shù))
預(yù)計全年級恰有2000名學(xué)生,正式測試每分鐘跳182個以上的人數(shù);(結(jié)果四舍五入到整數(shù))
![]() 若在全年級所有學(xué)生中任意選取3人,記正式測試時每分鐘跳195以上的人數(shù)為ξ,求隨機變量的分布列和期望.
若在全年級所有學(xué)生中任意選取3人,記正式測試時每分鐘跳195以上的人數(shù)為ξ,求隨機變量的分布列和期望.
附:若隨機變量![]() 服從正態(tài)分布
服從正態(tài)分布![]() ,則
,則![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】古希臘雅典學(xué)派算學(xué)家歐道克薩斯提出了“黃金分割”的理論,利用尺規(guī)作圖可畫出己知線段的黃金分割點,具體方法如下:(l)取線段AB=2,過點B作AB的垂線,并用圓規(guī)在垂線上截取BC=![]() AB,連接AC;(2)以C為圓心,BC為半徑畫弧,交AC于點D;(3)以A為圓心,以AD為半徑畫弧,交AB于點E.則點E即為線段AB的黃金分割點.若在線段AB上隨機取一點F,則使得BE≤AF≤AE的概率約為( )(參考數(shù)據(jù):
AB,連接AC;(2)以C為圓心,BC為半徑畫弧,交AC于點D;(3)以A為圓心,以AD為半徑畫弧,交AB于點E.則點E即為線段AB的黃金分割點.若在線段AB上隨機取一點F,則使得BE≤AF≤AE的概率約為( )(參考數(shù)據(jù):![]() 2.236)
2.236)
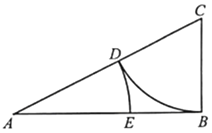
A. 0.236B. 0.382C. 0.472D. 0.618
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某公交公司為了方便市民出行、科學(xué)規(guī)劃車輛投放,在一個人員密集流動地段增設(shè)一個起點站,為研究車輛發(fā)車間隔時間![]() (分鐘)與乘客等候人數(shù)
(分鐘)與乘客等候人數(shù)![]() (人)之間的關(guān)系,經(jīng)過調(diào)查得到如下數(shù)據(jù):
(人)之間的關(guān)系,經(jīng)過調(diào)查得到如下數(shù)據(jù):
間隔時間 |
|
|
|
|
|
|
等候人數(shù) |
|
|
|
|
|
|
調(diào)查小組先從這![]() 組數(shù)據(jù)中選取
組數(shù)據(jù)中選取![]() 組數(shù)據(jù)求線性回歸方程,再用剩下的
組數(shù)據(jù)求線性回歸方程,再用剩下的![]() 組數(shù)據(jù)進行檢驗.檢驗方法如下:先用求得的線性回歸方程計算間隔時間對應(yīng)的等候人數(shù)
組數(shù)據(jù)進行檢驗.檢驗方法如下:先用求得的線性回歸方程計算間隔時間對應(yīng)的等候人數(shù)![]() ,再求
,再求![]() 與實際等候人數(shù)
與實際等候人數(shù)![]() 的差,若差值的絕對值不超過
的差,若差值的絕對值不超過![]() ,則稱所求線性回歸方程是“恰當(dāng)回歸方程”.
,則稱所求線性回歸方程是“恰當(dāng)回歸方程”.
(1)從這![]() 組數(shù)據(jù)中隨機選取
組數(shù)據(jù)中隨機選取![]() 組數(shù)據(jù)后,求剩下的
組數(shù)據(jù)后,求剩下的![]() 組數(shù)據(jù)的間隔時間之差大于
組數(shù)據(jù)的間隔時間之差大于![]() 的概率;
的概率;
(2)若選取的是后面![]() 組數(shù)據(jù),求
組數(shù)據(jù),求![]() 關(guān)于
關(guān)于![]() 的線性回歸方程
的線性回歸方程![]() ,并判斷此方程是否是“恰當(dāng)回歸方程”;
,并判斷此方程是否是“恰當(dāng)回歸方程”;
(3)在(2)的條件下,為了使等候的乘客不超過![]() 人,則間隔時間最多可以設(shè)置為多少分鐘?(精確到整數(shù))
人,則間隔時間最多可以設(shè)置為多少分鐘?(精確到整數(shù))
參考公式: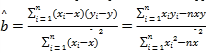 ,
,![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
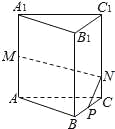
【題目】如圖,在正三棱柱![]() 中,AB=3,
中,AB=3,![]() =4,M為
=4,M為![]() 的中點,P是BC邊上的一點,且由點P沿棱柱側(cè)面經(jīng)過棱
的中點,P是BC邊上的一點,且由點P沿棱柱側(cè)面經(jīng)過棱![]() 到M點的最短路線長為
到M點的最短路線長為![]() ,設(shè)這條最短路線與
,設(shè)這條最短路線與![]() 的交點為N,求
的交點為N,求
(1)該三棱柱的側(cè)面展開圖的對角線長.
(2)PC和NC的長
(3)平面NMP與平面ABC所成二面角(銳角)的大小(用反三角函數(shù)表示)
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() .
.
(1)討論函數(shù)![]() 的單調(diào)性;
的單調(diào)性;
(2)若函數(shù)![]() 在
在![]() 處取得極值,不等式
處取得極值,不等式![]() 對
對![]() 恒成立,求實數(shù)
恒成立,求實數(shù)![]() 的取值范圍;
的取值范圍;
(3)當(dāng)![]() 時,證明不等式
時,證明不等式![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】(本小題滿分13分) 已知雙曲線![]() 的兩個焦點為
的兩個焦點為![]() 的曲線C上.
的曲線C上.
(Ⅰ)求雙曲線C的方程;
(Ⅱ)記O為坐標(biāo)原點,過點Q(0,2)的直線l與雙曲線C相交于不同的兩點E、F,若△OEF的面積為![]() 求直線l的方程
求直線l的方程
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知直線![]() :
:![]() 與焦點為
與焦點為![]() 的拋物線
的拋物線![]() :
:![]() 相切.
相切.
(Ⅰ)求拋物線![]() 的方程;
的方程;
(Ⅱ)過點![]() 的直線
的直線![]() 與拋物線
與拋物線![]() 交于
交于![]() ,
,![]() 兩點,求
兩點,求![]() ,
,![]() 兩點到直線
兩點到直線![]() 的距離之和的最小值.
的距離之和的最小值.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com