
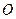 為原點(diǎn)的直角坐標(biāo)系中,點(diǎn)
為原點(diǎn)的直角坐標(biāo)系中,點(diǎn)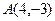 為
為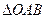 的直角頂點(diǎn),若
的直角頂點(diǎn),若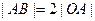 ,且點(diǎn)
,且點(diǎn)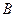 的縱坐標(biāo)大于0
的縱坐標(biāo)大于0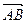 的坐標(biāo);
的坐標(biāo);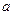 ,使得拋物線
,使得拋物線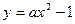 上總有關(guān)于直線
上總有關(guān)于直線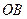 對稱的兩個(gè)點(diǎn)?若存在,求實(shí)數(shù)
對稱的兩個(gè)點(diǎn)?若存在,求實(shí)數(shù)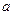 的取值范圍,若不存在,說明理由.
的取值范圍,若不存在,說明理由. (2)當(dāng)
(2)當(dāng) 時(shí),拋物線
時(shí),拋物線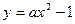 上總有關(guān)于直線
上總有關(guān)于直線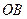 對稱的兩個(gè)點(diǎn)
對稱的兩個(gè)點(diǎn) 
 ,得
,得 ……(4分)
……(4分) 或
或 ……(5分)
……(5分) ,
,
 ……(7分)
……(7分) 為拋物線上關(guān)于直線
為拋物線上關(guān)于直線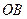 對稱的兩點(diǎn),
對稱的兩點(diǎn), , 又因?yàn)?img src="http://thumb.zyjl.cn/pic2/upload/papers/20140823/20140823135941029661.gif" style="vertical-align:middle;" />
, 又因?yàn)?img src="http://thumb.zyjl.cn/pic2/upload/papers/20140823/20140823135941029661.gif" style="vertical-align:middle;" /> …………(10分)
…………(10分) 為方程
為方程 的兩個(gè)相異實(shí)根
的兩個(gè)相異實(shí)根 ,可得
,可得
 時(shí),拋物線
時(shí),拋物線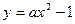 上總有關(guān)于直線
上總有關(guān)于直線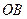 對稱的兩個(gè)點(diǎn)…(13分)
對稱的兩個(gè)點(diǎn)…(13分)

 名師點(diǎn)睛字詞句段篇系列答案
名師點(diǎn)睛字詞句段篇系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源:不詳 題型:解答題
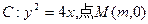 在x軸的正半軸上,過M的直線
在x軸的正半軸上,過M的直線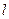 與C相交于A、B兩點(diǎn),O為坐標(biāo)原點(diǎn)。
與C相交于A、B兩點(diǎn),O為坐標(biāo)原點(diǎn)。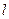 的斜率為1,求以AB為直徑的圓的方程;
的斜率為1,求以AB為直徑的圓的方程;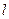 繞點(diǎn)M如何轉(zhuǎn)動(dòng),使得
繞點(diǎn)M如何轉(zhuǎn)動(dòng),使得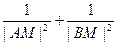 恒為定值。
恒為定值。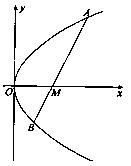
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:不詳 題型:解答題
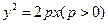 的焦點(diǎn)與橢圓
的焦點(diǎn)與橢圓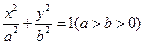 的一個(gè)焦點(diǎn)重合,且拋物線與橢圓的一個(gè)交點(diǎn)為
的一個(gè)焦點(diǎn)重合,且拋物線與橢圓的一個(gè)交點(diǎn)為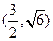 ,(1)求拋物線與橢圓的方程,(2)若過點(diǎn)
,(1)求拋物線與橢圓的方程,(2)若過點(diǎn)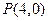 的直線與拋物線交于點(diǎn)
的直線與拋物線交于點(diǎn)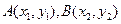 ,求
,求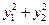 的最小值
的最小值查看答案和解析>>
科目:高中數(shù)學(xué) 來源:不詳 題型:填空題
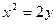
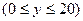 ,在杯中放入一個(gè)球,要使球觸及酒杯的底部,則球的半徑
,在杯中放入一個(gè)球,要使球觸及酒杯的底部,則球的半徑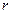 的取值范圍是 。
的取值范圍是 。查看答案和解析>>
科目:高中數(shù)學(xué) 來源:不詳 題型:解答題
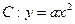 ,點(diǎn)P(1,-1)在拋物線C上,過點(diǎn)P作斜率為k1、k2的兩條直線,分別交拋物線C于異于點(diǎn)P的兩點(diǎn)A(x1,y1),B(x2,y2),且滿足k1+k2=0.
,點(diǎn)P(1,-1)在拋物線C上,過點(diǎn)P作斜率為k1、k2的兩條直線,分別交拋物線C于異于點(diǎn)P的兩點(diǎn)A(x1,y1),B(x2,y2),且滿足k1+k2=0.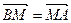 ,求點(diǎn)M的軌跡方程.
,求點(diǎn)M的軌跡方程.查看答案和解析>>
科目:高中數(shù)學(xué) 來源:不詳 題型:解答題
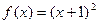
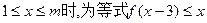 恒成立,求實(shí)數(shù)m的最大值;
恒成立,求實(shí)數(shù)m的最大值;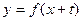 上存在兩點(diǎn)關(guān)于直線
上存在兩點(diǎn)關(guān)于直線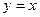 對稱,求t的取值范圍;
對稱,求t的取值范圍;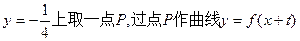 的兩條切線l1、l2,
的兩條切線l1、l2,查看答案和解析>>
科目:高中數(shù)學(xué) 來源:不詳 題型:填空題
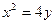 的焦點(diǎn)為F,準(zhǔn)線與y軸的交點(diǎn)為M,N為拋物線上的一點(diǎn),且
的焦點(diǎn)為F,準(zhǔn)線與y軸的交點(diǎn)為M,N為拋物線上的一點(diǎn),且 。
。查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com